Przeglądam na bieżąco strony internetowe dedykowane systemom CAD. Na jednym z blogów znalazłem opis problemu z takim komentarzem: „I to jest właśnie piękno CATII – już dawno przestałem myśleć, że się czegoś nie da zrobić – po prostu prawdopodobnie nie znam na to jeszcze odpowiedniej metody.”

Andrzej Wełyczko

Problem polegał na znalezieniu takiego punktu zadanej krzywej, w którym promień krzywizny jest najmniejszy. Zadanie wydaje się trywialne, ale... w systemie CATIA V5 nie ma polecenia, które wyznacza taki punkt. Za pomocą odpowiedniej formuły obliczeniowej można zdefiniować wartość minimalnego promienia krzywizny wskazanej krzywej (Rys. 1) – tu parametr MinCurvRadius = minimumCurvatureRadius(‘Geometrical Set.1\MyCurve‘) dla krzywej MyCurve. Za pomocą polecenia Porcupine Curvature Analysis można otrzymać rozkład krzywizny lub promienia krzywizny tej krzywej w każdym jej punkcie, ale nie można zdefiniować punktu z minimalnym promieniem krzywizny.

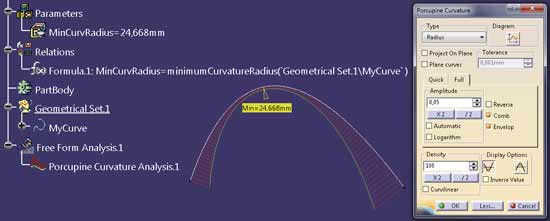
Rys. 1

Można oczywiście pokornie przyjąć do wiadomości taki „brak” i zapomnieć o problemie lub zastanowić się nad opracowaniem metody, która rozwiąże problem. Pierwszym i trochę prymitywnym rozwiązaniem może być metoda iteracyjna, w której położenie poszukiwanego punktu jest ustalone „ręcznie”. Dla dowolnego punktu XPoint krzywej MyCurve za pomocą odpowiedniej formuły obliczeniowej można określić promień krzywizny w tym punkcie (Rys. 2): XPointRadius = 1mm/curvature(‘Geometrical Set.1\MyCurve‘, ‘Geometrical Set.1\XPoint‘).

Rys. 2

Zadanie polega na znalezieniu takiej wartości współrzędnej Ratio punktu XPoint, dla której wartości parametrów xPointRadius i MinCurvRadius są równe. Po wykonaniu polecenia Porcupine Curvature Analysis wiemy przecież w jakiej części analizowanej krzywej znajduje się poszukiwany punkt (tu wstępnie ustalono Ratio = 0,22), a potem z małym krokiem (na przykład Step = 0,0001) ustalić taką wartość parametru Ratio, dla której parametry MinCurvRadius i xPointRadius mają równe wartości (Rys. 3).

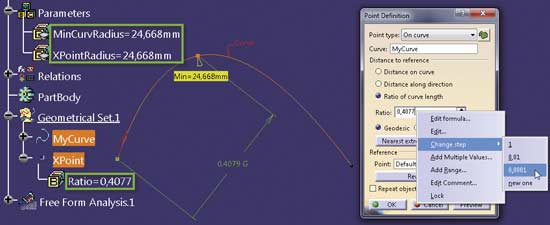
Rys. 3

Nic trudnego, ale czy nie można byłoby „zmusić” CATII do tego, aby taki punkt był wyznaczony automatycznie?

Poszukiwanie punktu krzywej z minimalnym promieniem krzywizny jest typowym zadaniem optymalizacyjnym i dlatego kolejna metoda korzysta z możliwości jakie daje polecenie Optimization w środowisku Product Engineering Optimizer (Rys. 4).

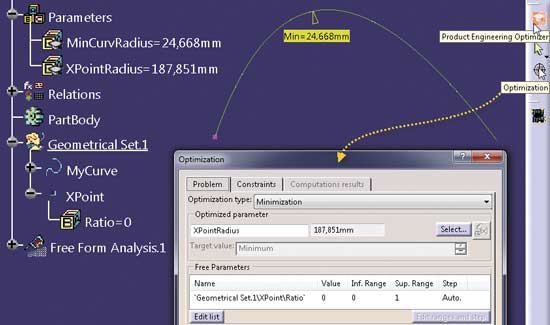
Rys. 4

Definicja zadania optymalizacyjnego jest w tym przypadku bardzo oczywista:

• Funkcja celu: minimalizacja wartości parametru xPointRadius. Uwaga: Możliwe jest zdefiniowanie parametru pomocniczego Delta, którego wartość będzie obliczona za pomocą formuły: Delta = 1mm/curvature(‘Geometrical Set.1\MyCurve‘ ,‘Geometrical Set.1\XPoint‘) – minimumCurvatureRadius(‘Geometrical Set.1\MyCurve‘). W takim przypadku zadanie optymalizacyjne polega na znalezieniu takiej wartości parametru swobodnego, dla którego Delta = 0mm, czyli Optimization type: Target Value, Optimized parameter: Delta oraz Target value = 0mm.
• Parametr swobodny: współrzędna Ratio punktu xPoint.

Zaleca się ustalenie dozwolonego zakresu wartości dla parametrów swobodnych, aby uniknąć poszukiwania rozwiązania optymalnego dla wartości generujących rozwiązania nielogiczne z konstrukcyjnego punktu widzenia. Z tego powodu dla parametru Ratio ustalono Inf. Range = 0 i Sup. Range = 1.
Mniej oczywisty jest wybór algorytmu optymalizacji oraz kryteriów zakończenia obliczeń. Spośród pięciu dostępnych algorytmów (Rys. 5) w tym przypadku należy rozważyć zastosowanie jednego z dwóch: Gradient Algorithm Without Constraints oraz Simulated Annealing Algorithm.

Rys. 5

Pozostałe algorytmy są dedykowane do rozwiązywania zadań optymalizacyjnych, w których zdefiniowano dodatkowe ograniczenia (Constraints), czyli zależności pomiędzy parametrami swobodnymi.
Simulated Annealing Algorithm poszukuje rozwiązania optymalnego w całej przestrzeni wyznaczonej przez parametry swobodne, a obliczenia są zakończone dopiero wtedy, gdy jedno z kryteriów zatrzymania optymalizacji zostanie spełnione. Obliczenia metodą Gradient Algorithm Without Constraints są zakończone po znalezieniu optimum lokalnego, niezależnie od tego, czy kryteria zatrzymania optymalizacji są spełnione czy nie. Dla krzywej z jednym ekstremum zastosowanie dowolnego z tych dwóch algorytmów kończy się wyznaczeniem szukanego minimum. Na przykład dla Gradient Algorithm Without Constraints punkt z minimalnym promieniem krzywizny zostaje znaleziony dla domyślnych kryteriów zakończenia obliczeń (Rys. 6).

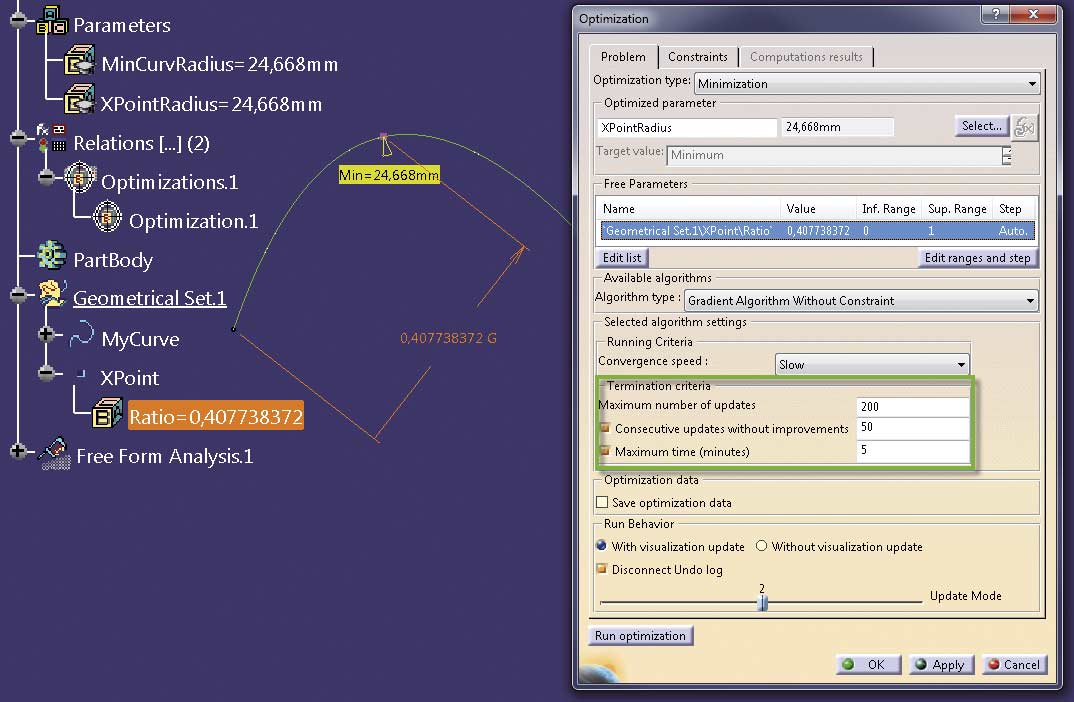Rys. 6

Nie muszę chyba dodawać, że parametr MinCurvRadius oraz analiza Porcupine Curvature Analysis.1 nie są konieczne do wykonania zadania optymalizacyjnego, czyli znalezienia punktu krzywej z minimalnym promieniem krzywizny. Zostały one zdefiniowane po to, aby mieć możliwość porównania z wynikami optymalizacji.