Wzrost mocy obliczeniowej komputerów w ostatnich latach pozwolił znacznie zredukować czas potrzebny do wykonania obliczeń numerycznych. Dodatkowo możliwe stało się przeprowadzanie obliczeń wcześniej nieosiągalnych na średniej klasy sprzęcie komputerowym. Jednak pomimo znacznej poprawy w tym zakresie, coraz częściej wykorzystuje się metody upraszczania problemów obliczeniowych w celu dalszej redukcji czasu obliczeń, jak również zmniejszenia skomplikowania modeli.
Maciej Majerczak
Jednym ze sposobów „odchudzenia” modelu obliczeniowego jest wykorzystanie substruktur. Bardzo często słowo substruktura jest zamiennie używane w odniesieniu do superelementów. Termin substruktura oznacza superelement, dla którego możliwe jest późniejsze odzyskanie wyników w danej substrukturze, dla modelu pełnego. Metoda substruktur w dużym uproszczeniu polega na przygotowaniu pełnego modelu MES, a następnie obliczeniu tzw. substruktury, czyli modelu zastępczego, odzwierciedlającego pierwowzór, ale w znacznie uproszczony sposób.
W tym artykule skupimy się na ogólnym opisie metody oraz jej wykorzystaniu w oprogramowaniu Abaqus. W następnej części przedstawiony zostanie sposób uzyskania podobnych superelementów w oprogramowaniu Nastran/Optistruct oraz ich wykorzystanie w innych typach analiz.
Czym są substruktury/superelementy?
Bazując na definicji substruktury znajdującej się w dokumentacji Abaqusa: „Substruktury są zbiorem elementów zgrupowanych razem, gdzie wewnętrzne stopnie swobody dla danej grupy zostały zredukowane na potrzeby analizy”. Oznacza to, że generując substrukturę, świadomie pozbywamy się pewnych informacji z modelu ale w sposób zaplanowany i kontrolowany. W zamian otrzymujemy model uproszczony, pozwalający na wielokrotne wykorzystanie w jednej analizie (na przykład jako złożenie substruktur), w analizach iteracyjnych (gdzie ważne jest możliwie wysokie uproszczenie modeli) lub w analizach z powtarzającymi się komponentami ale w różnych przypadkach obliczeniowych tzw. LoadCases.
Poniżej przedstawiono główne zalety metody bazującej na wykorzystaniu substruktur:
- Redukcja kosztów i czasu – związana jest zarówno ze zmniejszeniem czasu potrzebnego do obliczeń, jak również zasobów. Redukcja czasu może wywodzić się przykładowo z przygotowania pewnej substruktury, a następnie wielokrotnym jej wykorzystaniu podczas różnego rodzaju obliczeń. Należy również pamiętać, że sama substruktura jest już uproszczeniem, dlatego czas jej obliczeń jest krótszy, a potrzebne zasoby obliczeniowe mniejsze w porównaniu do pełnego modelu.
- Szybszy dostęp do obliczeń – Każdy inżynier zajmujący się obliczeniami numerycznymi spotkał się z problemem kolejkowania zadań. Są one spowodowane brakiem zasobów sprzętowych lub licencji. Wykorzystując substruktury znacznie skracamy czasy obliczeń oraz ilość potrzebnych zasobów, przez co skracamy kolejki i zwiększamy wydajność.
- Redukcja ryzyka – Przygotowując substrukturę wykonujemy jej jednokrotną analizę; oznacza to, że wykorzystując już wcześniej policzoną substrukturę, nie narazimy się na wystąpienie błędu w zastąpionym wcześniej złożeniu. Dodatkowo mamy pewność, że dana część naszego modelu jest niezmieniona i zawsze taka sama dla wszystkich wykonywanych przez nas obliczeń.
- Możliwość analizy dużych zadań – Wykorzystanie substruktur pozwala na obliczenia bardzo dużych zadań z interesującą nas dokładnością. Sam pomysł substruktur pojawił się w obliczeniach dużych i nieraz bardzo skomplikowanych maszyn, jakimi są np. samoloty. Wykorzystując substruktury możliwe jest podzielenie ogromnego złożenia na elementy składowe, wykonanie obliczeń dla mniejszych struktur, a następnie złożenie wszystkiego w całość, przy uwzględnieniu wzajemnych interakcji.
- Fragmentacja danych – Wykonując analizy z wykorzystaniem substruktury możliwe jest bardzo łatwe zarządzanie zarówno danymi wejściowymi, jak również wyjściowymi. W prosty sposób można podmieniać substruktury występujące w modelu, jak również szybko przeliczać wyniki tylko dla interesujących nas komponentów spośród całego złożenia.
Rysunek 1 przedstawia wykorzystanie substruktury jednego zęba w kole zębatym (pozostałe zęby przekładni są tą samą substrukturą wykorzystaną ponownie).
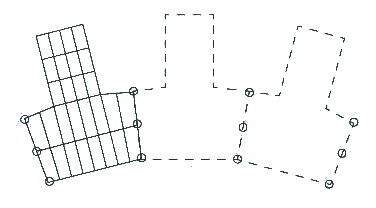
Rys. 1 Schematyczne przedstawienie wykorzystania substruktury zęba w kole zębatym
Przygotowanie substruktury w oprogramowaniu Abaqus
Przygotowanie modelu do wyliczenia substruktury praktycznie nie różni się od normalnego przygotowania modelu MES. Dlatego dobrą praktyką jest sporządzenie prostej analizy statycznej lub modalnej naszego modelu, w celu sprawdzenia poprawności przygotowanego zadania.
Po udanym przygotowaniu analizy można rozpocząć prace nad substrukturą. W sieci znajduje się kilka tutoriali, w których wykorzystywane jest środowisko Abaqus CAE, jednak w artykule zdecydowano się przedstawić manualny sposób uzyskania tego samego efektu poprzez ręczną edycję plików .inp.
Na początku, do naszego modelu należy dodać dodatkowy set węzłowy. W zbiorze tym powinny się znaleźć węzły, które chcemy pozostawić w modelu substruktury. Przeważnie są to węzły, przy pomocy których dokonywane będzie przyłączenie substruktury do reszty modelu, lub miejsca będące „czujnikami”, w których zbierane będą dane. Należy jednak pamiętać, że wraz ze wzrostem ilości węzłów, które chcemy pozostawić, znacząco rośnie czas obliczeń, jak również rozmiar plików substruktury.
Następnie należy rozważyć jakiego rodzaju substrukturę będziemy chcieli wykorzystać do naszych dalszych obliczeń. W Abaqusie rozróżnić można pełną substrukturę, gdzie informacje zapisane są w plikach .sup .sim .prt .stt oraz .mdl, jak również znacznie uproszczony model zawierający jedynie opis danej substruktury w postaci macierzy .mtx.
Zajmijmy się na początku metodą uproszczoną. Polega ona na wygenerowaniu przez solver pliku zawierającego macierze, w pełni odzwierciedlające interesujący nas układ. W zależności jakie obliczenia będą wykonywane w przyszłości, można zlecić aby algorytm przygotował macierze sztywności, masy oraz tłumienia. Warto tutaj zauważyć, że rozmiar uzyskiwanych macierzy zależy wprost od ilości węzłów znajdujących się we wcześniej opisywanym zbiorze węzłów (ilość kolumn oraz wierszy w macierzy równa jest ilości węzłów pozostawionych w substrukturze). Macierze zostaną zapisane w formacie tekstowym w pliku .mtx. Plik ten jest zdecydowanie mniejszy od plików potrzebnych dla pełnej substruktury, jednak przy jego wykorzystaniu nie jest możliwa analiza wyników dla samej substruktury.
Poniżej przedstawiono fragment kodu potrzebnego do wygenerowania tego typu substruktury:
*STEP
*SUBSTRUCTURE GENERATE, TYPE=Z0002, MASS MATRIX=YES
*SUBSTRUCTURE MATRIX OUTPUT,FILE NAME=abaqus_substructure_file, STIFFNESS=YES, MASS=YES
*RETAINED NODAL DOFS
ASET
*END STEP
Następnie powstały superelement, opisany przy pomocy macierzy, można zaimplementować do złożenia poprzez wykorzystanie userelementów w Abaqusie. Odpowiedni kod należy dodać do pliku .inp, w którym wykorzystywana będzie substruktura zawarta w pliku .mtx. Polecenie to zawiera opis typu elementu, jego numer oraz wszystkie węzły zawierające się w tym elemencie (Rys. 2).
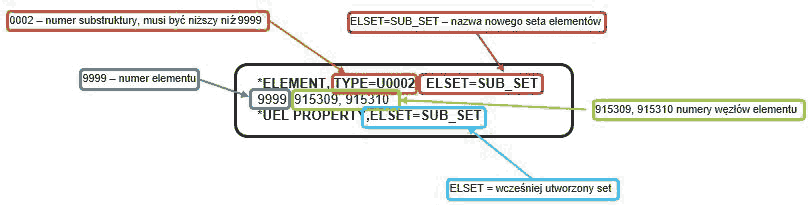
Rys. 2 Składnia oraz opis poszczególnych komponentów potrzebnych do zaimportowania substruktury
W celu wykonania poprawnego importu substruktury do naszego modelu należy również wprowadzić polecenie dołączenia pliku .mtx do pliku głównego .inp. Odbywa się to przez keyword *INCLUDE. W pliku .mtx należy także dodać typ userelementu. Dla tej metody będzie to TYPE=Uxxxx.
Drugim sposobem wykorzystania substruktury jest implementacja całej bazy dostępnej po obliczeniach substruktury. Takie podejście pozwala na pełne wykorzystanie zalet tej metody, jednak rozmiar substruktury utworzonej w ten sposób jest znacznie większy, w porównaniu do metody opartej na macierzach zawartych w plikach .mtx. Metoda ta pozwala też w szybki sposób przeprowadzić konwersję substruktury wygenerowanej w Abaqusie do substruktur, rozpoznawanych przez solvery Nastran oraz Optistruct.
Do implementacji tego typu substruktury w oprogramowaniu Abaqus wymagane są pliki wygenerowane podczas obliczeń samej substruktury i są to pliki: .sup .sim .prt .stt oraz .mdl. Pierwszy z plików ma nazwę analogiczną do nazwy modelu .inp, natomiast pozostałe mają na końcu nazwy przyrostek z nazwą substruktury, np. xxx_Z0002.xxx (Rys. 3).
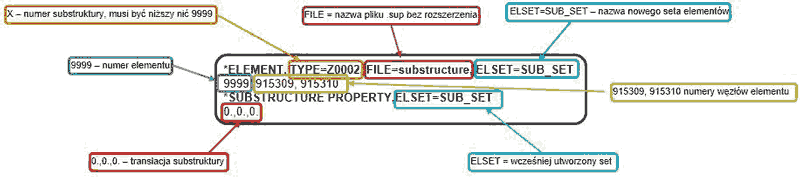
Rys. 3 Składnia oraz opis poleceń potrzebnych do zaimportowania pełnej substruktury
Model testowy oraz analiza wyników
Obliczenia oraz porównanie wyników zostało przedstawione dla bardzo prostego modelu wiatraczka, pobranego z portalu GrabCAD. Oczywiście, podobne podejście może zostać zastosowane również dla znacznie bardziej skomplikowanych struktur. Na rysunku 4 został przedstawiony model CAD analizowanego złożenia. W celu redukcji czasu obliczeń, w wielu miejscach zastosowano wspólną siatkę, tak aby uniknąć zasobożernych połączeń typu TIE.
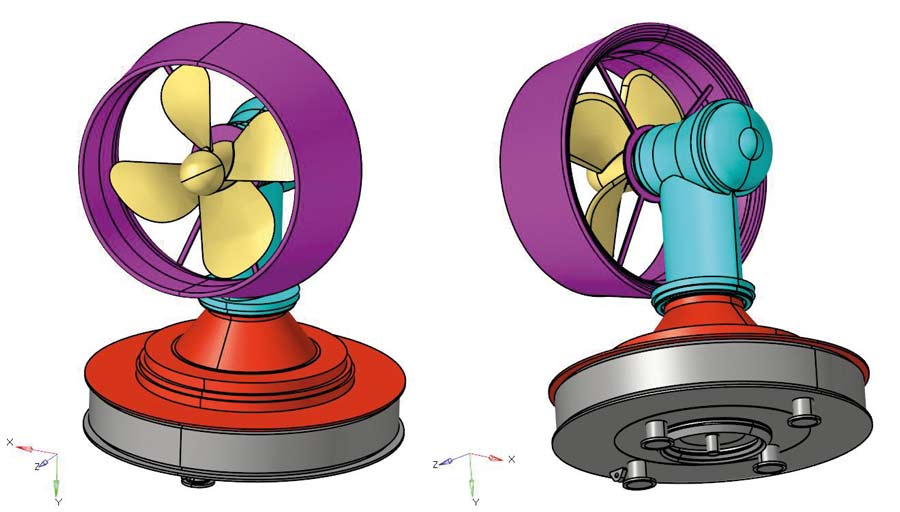
Rys. 4 Modele CAD analizowanego komponentu
Dla analizowanego modelu zdecydowano się na zastąpienie substrukturą dwóch komponentów podstawy, to jest czerwonej oraz szarej podstawki, pomiędzy którymi zastosowano połączenie TIE (Rys. 5).
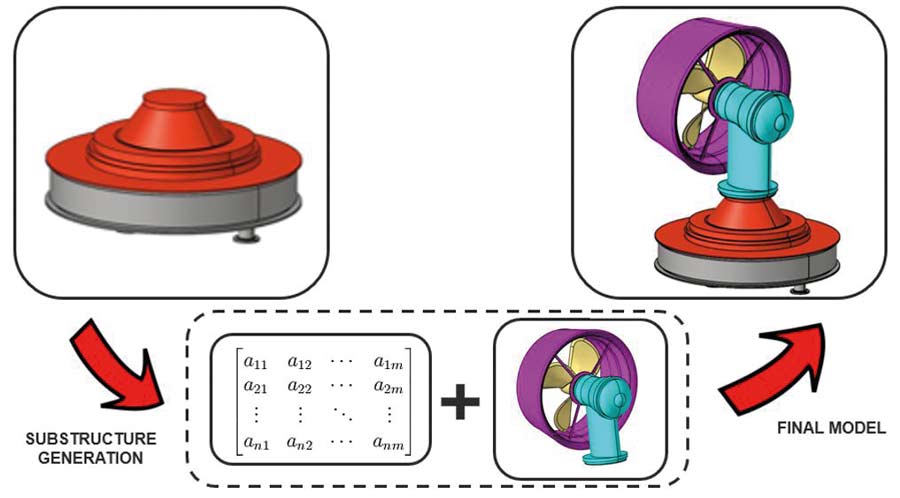
Rys. 5 Schemat przygotowania modelu przy pomocy substruktur
Tak jak wspomniano wcześniej, w celu przygotowania substruktury podstawy wiatraka, przeprowadzono najpierw obliczenia sprawdzające dla całego modelu. Zdecydowano się na analizę modalną, ponieważ analizując wyniki tego typu analizy można wychwycić większość błędów powstałych podczas tworzenia modelu.
Na rysunku 6 przedstawiono porównanie wyników analizy modalnej dla wszystkich trzech modeli. Jak widać, uzyskane wyniki są bardzo do siebie zbliżone, zarówno dla modów lokalnych, jak również dla globalnych częstotliwości rezonansowych.
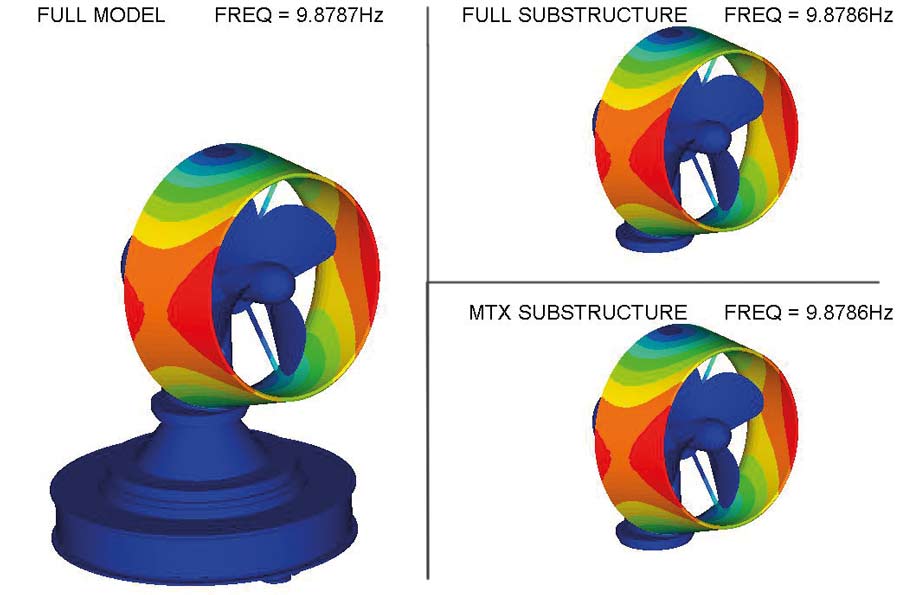
Rys. 6 Częstotliwości i postaci drgań własnych dla modu pierwszego
Tabela 1 przedstawia porównanie wszystkich obliczonych modów dla modelu pełnego oraz uproszczonych modeli z substrukturami. Większość modów jest praktycznie identyczna, tylko niektóre nieznacznie odbiegają od siebie. Wyniki te pozwalają stwierdzić, że dla przygotowanego uproszczonego modelu możliwe jest jego wykorzystanie w dalszych analizach, bez obaw o znaczne rozbieżności pomiędzy modelem pełnym a uproszczonym.
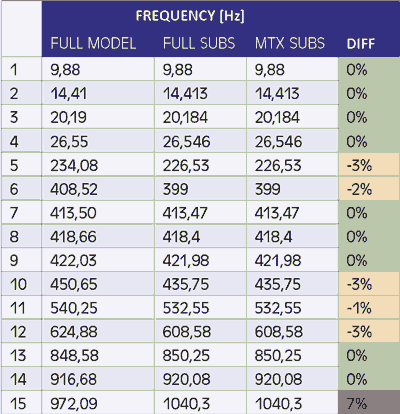
Tab. 1 Częstotliwości rezonansowe dla modeli uproszczonych oraz dla modelu pełnego
Podsumowanie
Opisana metoda jest bardzo interesującym rozwiązaniem dla wielu problemów inżynierskich. Dzięki odpowiedniemu przygotowaniu modelu i poprawnej implementacji substruktury możemy oszczędzić wiele czasu oraz zredukować zasoby potrzebne do wykonania obliczeń.
Przedstawione obliczenia zostały wykonane dla bardzo prostego modelu CAD, jednak metoda ta została również sprawdzona dla znacznie bardziej skomplikowanego modelu. Uzyskano również bardzo zadowalające wyniki, co pozwoliło później na wykorzystanie modelu z substrukturami do dalszych analiz.
W kolejnym artykule przedstawimy metodę wykorzystania substruktury w analizie optymalizacji konstrukcji z wykorzystaniem oprogramowania Optistruct.
Maciej Majerczak
Literatura:
ABAQUS 2017 HELP
https://grabcad.com
P.L.C. van der Valk: “Model Reduction & Interface Modeling in Dynamic Substructuring”, MSc. Thesis, 2014
“Using Substructures in Abaqus” [Online]: https://www.youtube.com/watch?v=APPgsHnaC2E
artykuł pochodzi z wydania 5 (140) maj 2019










