Jeśli zadaniem konstruktora jest definicja ewolwentowej powierzchni śrubowej, to należałoby się zastanowić skąd przymiotnik „ewolwentowa” w nazwie. Odpowiedź można łatwo znaleźć po analizie geometrycznej kolejnego modelu początkowego (Rys.14).
Andrzej Wełyczko
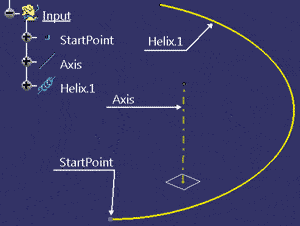
Rys. 14
W modelu tym zdefiniowane zostały następujące elementy:
- StartPoint – punkt początkowy krzywej śrubowej,
- Axis – oś krzywej śrubowej,
- Helix.1 – krzywa śrubowa,
W kolejnych krokach procedury konstrukcyjnej (Rys. 15) zdefiniowano:
- AnyPointOnHelix.1 – dowolny punkt na krzywej Helix.1,
- LineTangentToHelix.1 – linia styczna do krzywej Helix.1 w punkcie AnyPointOnHelix.1, o długości równej odległości punktu AnyPointOnHelix.1 od punktu StartPoint, mierzonej wzdłuż krzywej Helix.1,
- BaseCircle – ta krzywa może być zdefiniowana jako łuk okręgu o promieniu R lub jako rzut prostopadły krzywej Helix.1 na płaszczyznę (tu: xy plane) prostopadłą do osi krzywej Helix.1 (tu: linia Axis),
- AnyPointOnBaseCircle – rzut prostopadły punktu AnyPointOnHelix.1 na płaszczyznę prostopadłą do osi krzywej Helix.1,
- LineTangentToBaseCircle – linia styczna do krzywej BaseCircle w punkcie AnyPointOnBaseCircle, o długości równej odległości punktu AnyPointOnBaseCircle od punktu StartPoint, mierzonej wzdłuż krzywej BaseCircle.
Linia LineTangentToHelix.1 jest tworzącą ewolwentowej powierzchni śrubowej, a punkt końcowy linii LineTangentToBaseCircle wyznacza ewolwentę łuku BaseCircle. Pomiar odległości (MeasureBetween.1 \Length = 0mm) punktów końcowych linii LineTangentToHelix.1 i LineTangentToBaseCircle dowodzi, że te punkty są identyczne.
Wniosek: Krzywa brzegowa ewolwentowej powierzchni śrubowej jest ewolwentą łuku BaseCircle, lub inaczej – krzywa przecięcia ewolwentowej powierzchni śrubowej płaszczyzną prostopadłą do osi krzywej śrubowej tej powierzchni jest ewolwentą.
Jak zdefiniować krzywą ewolwentową dla zadanego łuku okręgu? Odpowiedź tu: Projektowanie i Konstrukcje Inżynierskie, czerwiec 6 (21) 2009: „Równanie krzywej i jej definicja w systemie CAD, część 3”. Niestety, choć metoda opisana przed laty generuje idealną ewolwentę, to jednak o ograniczonej długości. Krzywa zdefiniowana w ten sposób jest wystarczająco dobra do definicji kształtu powierzchni bocznej zęba w przekroju normalnym, ale nie ma praktycznego zastosowania w omawianym przykładzie. Dlatego jedynym rozwiązaniem (pomijam tu czysto programistyczne rozwiązania oparte na Visaul Basic lub C++) jest zastosowanie polecenia Knowledge Pattern, ale tym razem współrzędne punktów (punkt Pe na rysunku 16) generowanych w pętli konstrukcyjnej będą obliczone na podstawie równań ewolwenty.
cały artykuł dostępny jest w wydaniu 3 (90) marzec 2015










