Definicja punktu krzywej z minimalnym promieniem krzywizny; cz. 2

: Opublikowano: 17 lutego 2017

Wyznaczenie punktu krzywej z minimalnym promieniem krzywizny może być zrealizowane przez program obliczeniowy napisany na przykład w Visual Basic czy C++. Ani ja, ani pewnie większość użytkowników CATII nie ma czasu, chęci, doświadczenia ani rzeczywistej potrzeby zgłębiania tajników programowania. Chociaż muszę przyznać, że podstawowe umiejętności z tego zakresu przydają się bardzo podczas rozwiązywania problemów za pomocą narzędzi z grupy Knowledgeware.

Andrzej Wełyczko

Niezależnie od wybranej metody niezbędny jest pomysł, czyli mniej lub bardziej szczegółowy opis tego, co i jak chcemy zrobić. Może to być algorytm blokowy lub na przykład szkic kolejnych etapów poszukiwania rozwiązania optymalnego. Mój pomysł na rozwiązanie tego problemu nie jest chyba zbyt skomplikowany (Rys. 10):

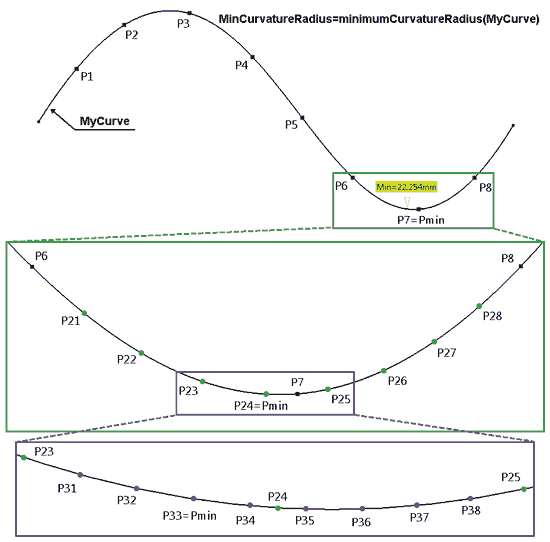
definicja punktu krzywej 10
Rys. 10

Za pomocą formuły obliczeniowej znajdź wartość minimalnego promienia krzywizny zadanej krzywej: MinCurvatureRadius = minimumCurvatureRadius(MyCurve)
Na zadanej krzywej zdefiniuj N punktów (tu: P1, P2, … P8) i w każdym z tych punktów oblicz promień krzywizny. Wybierz ten punkt, dla którego promień krzywizny jest najmniejszy (tu: P7=Pmin). Jeśli liczba punktów będzie odpowiednio duża, to ten punkt znajduje się w pobliżu minimum globalnego. UWAGA: Algorytm poszukiwania optimum musi być efektywny, a to oznacza, że liczba punktów nie może być ani za duża (czas obliczeń!), ani zbyt mała (dokładność wyznaczenia optimum!). Pojęcie „odpowiednio duża liczba punktów” będzie wyjaśnione później.
Skoro wstępnie ustalono położenie optimum, to trzeba ograniczyć poszukiwanie optimum do pewnego zakresu krzywej – tu: w pobliżu punktu P7. Poszukiwany punkt znajduje się na pewno pomiędzy punktami P6 i P8. Z tego powodu w kolejnej iteracji zdefiniuj kolejnych N punktów (tu: P21, P22, … P28), dla każdego z nich oblicz promień krzywizny i wybierz ten punkt, dla którego promień krzywizny jest najmniejszy (tu: P24=Pmin).
Jeśli promień krzywizny w punkcie P24=Pmin jest większy od wartości MinCurvatureRadius o mniej niż zadana dokładność (na przykład 0,001mm), to zakończ obliczenia. W przeciwnym przypadku powtórz procedurę opisaną w p. 3, czyli dla fragmentu krzywej w pobliżu punktu P24=Pmin (ograniczonej punktami P23 i P25) zdefiniuj N punktów (tu: P31, P32, … P38) i w każdym z tych punktów oblicz promień krzywizny. Wybierz ten punkt, dla którego promień krzywizny jest najmniejszy (tu: P33=Pmin)... itd.