Większości parametrycznych środowisk typu CAD pozwala swoim użytkownikom na tworzenie dwóch podstawowych rodzajów geometrii. Pierwszy oparty jest na bryłach, drugi na powierzchniach. Odzwierciedla to podejście do modelowania 3D opartego albo na modelowaniu bryłowym albo powierzchniowym. Połączenie obydwu ma miejsce w tak zwanym modelowaniu hybrydowym. Podstawowe narzędzia modelowania bryłowego, jak Wyciągniecie, Obrót, Przeciągniecie między przekrojami bądź po zdefiniowanej trajektorii, mają swoje ograniczenia w zakresie tworzenia powierzchni modelu o zmiennym przebiegu krzywizny (powierzchnie krzywokreślne). Takie powierzchnie wymagają wpierw przygotowania odpowiedniego układu krzywych.
Jacek Mydlikowski
Projektując produkty charakteryzujące się kształtami „krzywokreślnymi” (Rys. 1) użytkownik CAD może natknąć się na powierzchnie składające się z nieparzystej liczby krzywych. W przypadku braku odpowiednich narzędzi w środowisku CAD, przygotowanych do automatycznego i poprawnego rozwiązywania takich przypadków, użytkownicy powinni znać uniwersalne metody obchodzenia się takimi powierzchniami.
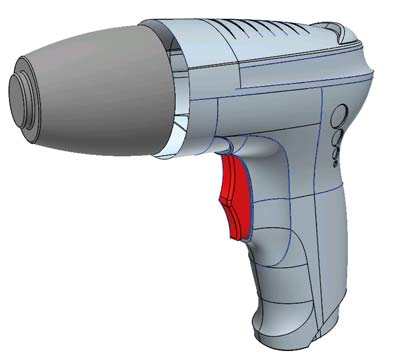
Rys. 1
Powierzchnie poprawne
Inżynierskie oprogramowanie CAD lubi powierzchnie analityczne, których opisanie staje się możliwe za pomocą podstawowych wzorów na okrąg, prostokąt, bądź całe bryły, jak walec lub prostopadłościan. Wspomniane kształty analityczne to domena głównie modelowania bryłowego. Dokładność takich obliczeń, a przez to samej geometrii jest doskonała. Stąd, rzadko występujące problemy w trakcie eksportu do STEP modeli opartych na poleceniach typu Wyciągnięcie lub Obrót. Modelowanie powierzchni krzywokreślnych, o zmiennej krzywiźnie, wykorzystuje powierzchnie typu NURBS, oparte na krzywych klejonych (Spline). W idealnej sytuacji powierzchnie typu NURBS składają się tylko z czterech brzegów (krawędzi lub krzywych). Mają one wówczas równomierny, jednorodny, rozkład kierunków UV. Na potrzeby tego artykułu będę takie powierzchnie nazywał poprawnymi (Rys. 2-3).

Rys. 2

Rys. 3
Każda powierzchnia potrzebująca mniej (minimum trzy) lub więcej brzegów staje się powierzchnią zaburzoną, będącą źródłem potencjalnych problemów w trakcie samego przygotowania, jak i późniejszych prac nad modelem. Będę je nazywał powierzchniami N-brzegowymi.
Powierzchnie N-brzegowe
Podstawowym przypadkiem powierzchni N-brzegowej będzie powierzchnia składająca się tylko z trzech brzegów. Będziemy ją nazywać trójbrzegową (Rys. 4).

Rys. 4
Domyślnie oparcie powierzchni typu NURBS jedynie na trzech brzegach spowoduje degenerację kierunków UV, wymuszając ich zbieganie się do jednego z wierzchołków, zaburzając w ten sposób równomierny rozkład. Taki wierzchołek nazwiemy zdegenerowanym (Rys. 5).
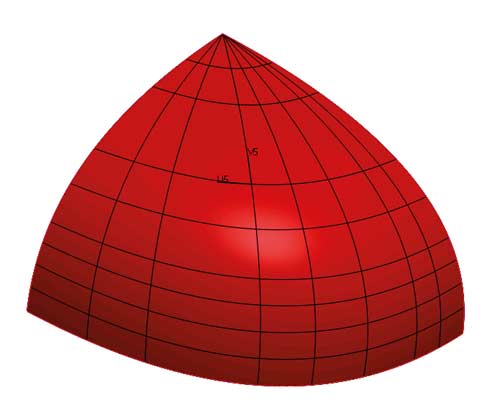
Rys. 5
Kolejnym przypadkiem powierzchni N-brzegowej będzie powierzchnia składająca się z pięciu brzegów. Będziemy nazywać ją pięciobrzegową (Rys. 6).

Rys. 6
Poza tymi dwoma podstawowymi odmianami zaburzonych powierzchni typu NURBS, użytkownicy CAD mogą natknąć się na powierzchnie sześciobrzegowe (Rys. 7).
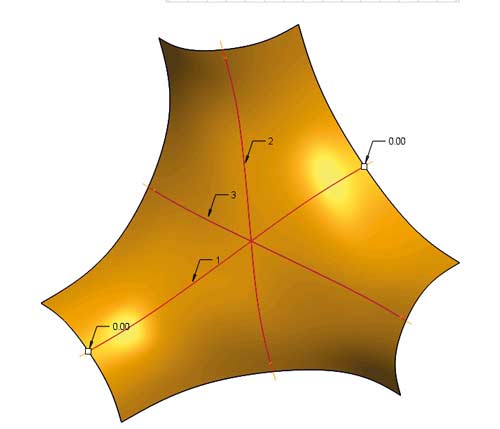
Rys. 7
Problemy
Napotkawszy wyzwanie związane z N-brzegową powierzchni możemy liczyć się z trzema rodzajami problemów. Pierwszy, coraz rzadszy, polega na braku dedykowanych narzędzi w aplikacji CAD do automatycznego i prawidłowego budowania takowych powierzchni. Na taki kłopot natknie się np. użytkownik środowiska Creo, które w podstawowym pakiecie nie udostępnia odpowiednich funkcji; stają się one dostępne dopiero po wykupieniu pakietu ISDX (np. prawidłowa powierzchnia trój-, pięcio-, sześciobrzegowa, lub po aktywacji ukrytych funkcji, jak „enable_obsoleted_features”.).
Drugi problem to niepożądane rozwiązanie wspomnianych zagadnień przez dedykowane narzędzia. Automatycznie rozwiązywane zagadnienia N-brzegowe, mogą (lecz nie muszą) mieć kłopoty z jednorodnym przebiegiem krzywizny na obszarze powstałej powierzchni, w postaci nagłych wgłębień, wybrzuszeń i tak dalej. Pomocna w lokalizacji takich zaburzeń staje się analiza krzywizny metodą Gaussa (Rys. 8).
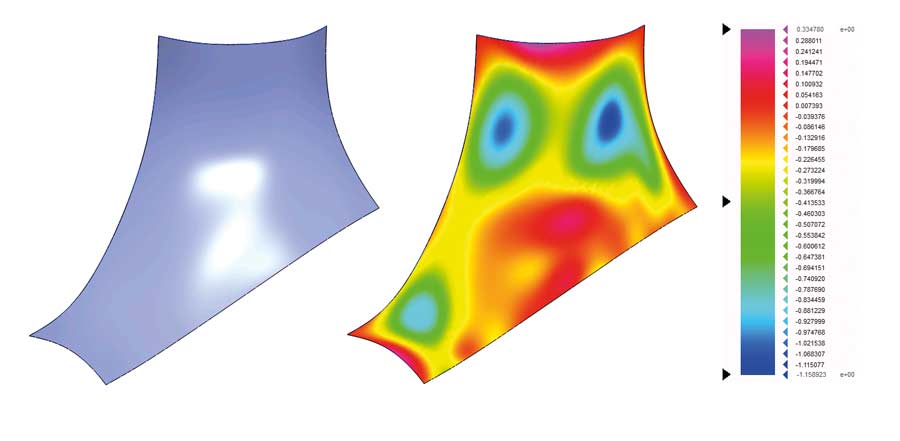
Rys. 8
Trzeci problem to dalsze prace w modelu, na przygotowanych powierzchniach zaburzonych. Powierzchnie o nierównomiernie rozłożonych kierunkach UV będą niejako mścić się podczas wszelakich operacji powielających. Zwłaszcza podczas generowania nowej powierzchni odsuniętej lub przy nadawaniu grubości (bryłowości) płatom powierzchni (na rysunku 9 – analiza odsunięcia zaburzonej powierzchni; w obu kierunkach są kłopoty).
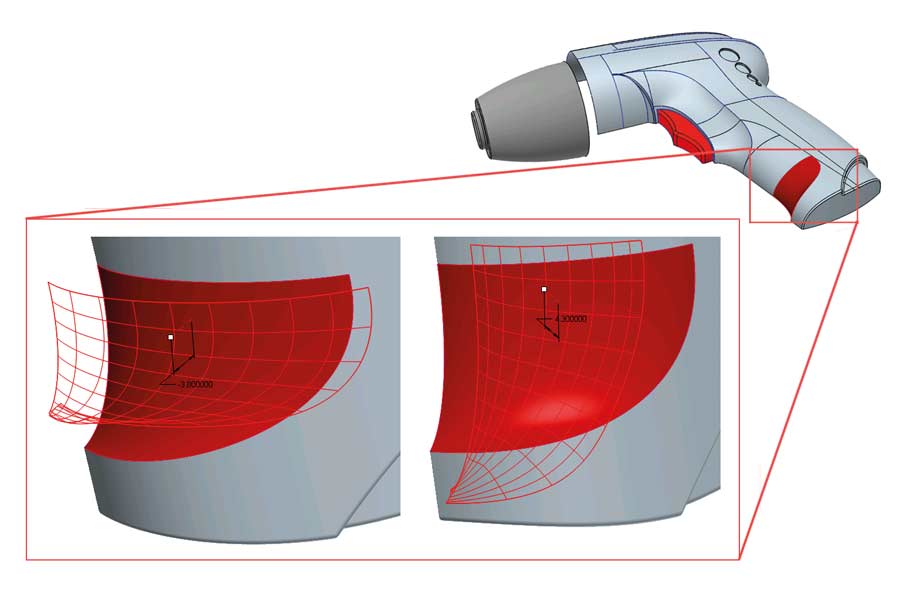
Rys. 9
Automatyczne rozwiązanie
Użytkownicy pracujący z CAD z aktywnymi narzędziami do pracy z zagadnieniami N-brzegowymi znajdują się w dość komfortowej sytuacji. Wspomniane narzędzia mają potencjał tworzenia dyskutowanych powierzchni z równomiernie rozłożonymi kierunkami UV. Pozwalają również na nakładanie warunków ciągłości powierzchni dla wskazanych brzegów. Rozwiązanie zagadnienia N-brzegowego w tych narzędziach następuje przez rozpięcie specjalnej powierzchni czterobrzegowej, docinanej następnie w wskazanych brzegach (Rys. 10-11).

Rys. 10

Rys. 11
Rozwiązania „ręczne”
W sytuacji braku dedykowanych narzędzi lub niezadowalających rezultatów ich zastosowania, użytkownicy dowolnego środowiska CAD mogą wykorzystać uniwersalną technikę dla rozwiązywania zagadnień N-brzegowych. Generalna zasada jest następująca: każde takie zagadnienie należy sprowadzić do powierzchni czterobrzegowej.
Omawianie powyższej techniki proponuję rozpocząć od powierzchni trójbrzegowej. W tym przypadku dysponujemy trzema możliwościami:
Wykorzystanie zdegenerowanej powierzchni – możemy wykorzystać istniejącą powierzchnię lub stworzyć ją samodzielnie, zdiagnozować położenie zdegenerowanego wierzchołka, wyciąć go, pozostawiając warunki czterobrzegowe, a następnie wypełnić brak poprawną powierzchnią. Aby wyciąć powierzchnię pierwotną należy na niej przygotować dwie krzywe, niestyczne do siebie. Można taki układ krzywych na powierzchnię zrzucić (Rys. 12-13).

Rys. 12

Rys. 13
- start
- Poprzedni artykuł
- 1
- 2
- Następny artykuł
- koniec






