Obiekt geometryczny może być wyświetlony w oknie Layout#1 w postaci Surface [powierzchnia], co odczytujemy w tytule zakładki na trzecim od góry pasku ekranu głównego. Do innej reprezentacji pola obliczeniowego przechodzimy wybierając w tej zakładce 3D glyphs [strzałki 3D], Outline [szkic], Points [punkty], Surface with edges [powierzchnia z krawędziami], Volume [objętość] albo Wireframe [siatka]. Rodzaj informacji wyświetlanej na kolorowo na obiekcie geometrycznym (w obszarze obliczeniowym) zmieniamy w innej zakładce trzeciego paska, która pierwotnie zawiera wybór vtkBlockColors [kolory bloków vtk]. Można tę opcję zmienić na Solid Color [kolor jednolity] albo na jeden z parametrów płynu, np. p [ciśnienie], U [pole prędkości], itd. (przy czym są do wyboru dwie metody prezentacji parametrów przepływowych: dane węzłowe – mały romb, dane uśredniane objętościowo – duży sześcian). Gdy parametr jest wielkością wektorową, w sąsiedniej zakładce mamy do wyboru opcje: Magnitude [moduł wektora] lub jedną z jego składowych X, Y albo Z. Po dokonaniu wyboru, wyświetli się w głównym oknie także kolorowa legenda, której zakres liczbowy można uaktualniać przyciskiem Rescale [przeskaluj], znajdującym się w oknie Properties, lub przyciskiem z zieloną obustronną strzałką – usytuowanym również na trzecim pasku okna głównego. Zestaw parametrów, możliwych do wyświetlania na obiekcie geometrycznym zależy od zaznaczenia dokonanego w zakładce Volume Fields [pola objętościowe] okna Properties (Rys. 9).

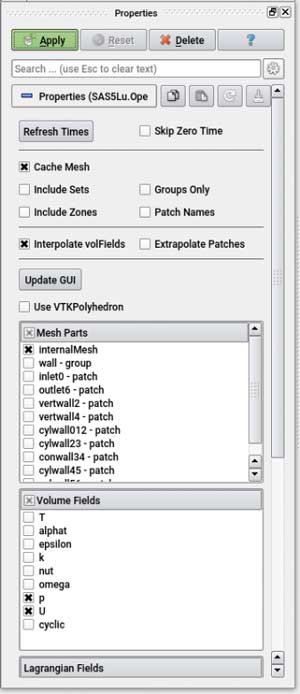
Rys. 9 Okno Properties umożliwia m.in. wybranie elementów składowych geometrii do wyświetlenia (Mesh Parts) oraz wybranie pól fizycznych do analizy (Volume Fields)

Legenda może być przesunięta w dowolne miejsce za pomocą myszy. Wyświetlany obiekt geometryczny obracamy za pomocą myszy albo manipulujemy nim za pomocą ikonek z trzeciego paska. Najczęściej używane sposoby modyfikacji geometrii to: Zoom to Box [powiększanie do ramki] oraz ukierunkowanie wzdłuż osi +X lub -X, itd. Cofnięcie operacji powiększenia uzyskujemy przyciskiem Reset (ikonka ze skrzyżowanymi strzałkami), a cofnięcie skutków manipulacji – za pomocą Camera Undo z zakładki głównej Edit. We wszystkich przypadkach nazwa funkcji realizowanej za pomocą ikonki wyświetlana jest po jej wskazaniu. Przy pomocy kombinacji przycisków F11/Esc (z klawiatury komputera) powiększymy okno graficzne do maximum lub cofniemy tę operację.

Przykład obliczeniowy
Wybrany do prezentacji przykład obliczeniowy przepływu powietrza przez rozgałęzienie przewodów opisywany jest za pomocą modelu płynu nieściśliwego, gazu doskonałego pod względem termodynamicznym. Zakłada się, że przepływ płynu ma charakter turbulentny, opisywany modelem RANS (Reynolds averaged Navier-Stokes) o nazwie kEpsilon, i jest to standardowy model Laundera i Spaldinga opisany w literaturze [1, 2]. Kanały mają przekrój kwadratowy o boku 0,02 m i długościach 0,2 m, a przekroje graniczne zdefiniowane są następująco: wlot inlet oraz wyloty outlet1 i outlet2. Warunki początkowe zdefiniowano za pomocą nadwyżki ciśnienia całkowitego, które w przekroju wlotowym wzrasta od wartości 10 do 40 m2/s2, a w przekrojach wylotowych utrzymywane jest na stałym poziomie 10 (outlet1) oraz 0 (outlet2). Pole prędkości scharakteryzowane jest na brzegach za pomocą zerowego gradientu lub zerowej wartości w przypadku napływu z zewnątrz. Równania przepływu rozwiązywane są algorytmem PIMPLE (zaimplementowanym w pakiecie pod nazwą pimpleFoam), który stanowi kombinację dwóch popularnych metod: SIMPLE [3] oraz PISO [4]. Obliczenia realizowane są z krokiem czasowym timeStep = 0.001 s, zapisywane w odstępach writeInterval = 0,1 s, do chwili końcowej endTime = 1,5 s. Maksymalna wartość liczby Couranta, stanowiącej kryterium stabilności obliczeń, wynosi maxCo = 5 (plik controlDict).
Wyniki obliczeń możemy analizować w sposób statyczny, wyświetlając dane z konkretnej chwili czasu, lub na sposób dynamiczny – wywołując ciągłą sekwencję danych. Pierwszy sposób realizowany jest przy wykorzystaniu standardowych ikonek sterujących „przewijaniem” danych, umieszczonych na drugim od góry pasku okna głównego, lub po prostu przez przestawienie cyfry reprezentującej kolejny krok czasowy – w sąsiednim okienku. Płynną sekwencję wyników obejrzymy po naciśnięciu ikonki >, a zatrzymamy standardowym przyciskiem pauzy ||. Przykładowy rozkład ciśnienia powietrza w kanale w chwili końcowej symulacji zilustrowano na rysunku 10.

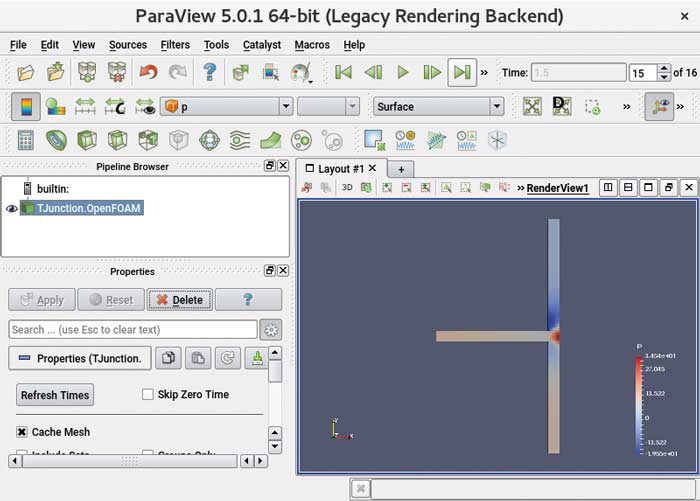
Rys. 10 Rozkład ciśnienia w obszarze obliczeniowym w chwili końcowej

Inną możliwością analizy wyników jest obserwacja linii prądu. Po wybraniu ikonki streamlineTracer i po wprowadzeniu jednej zmiany w oknie Properties, tzn. zmiany współrzędnej X punktu „zasiewu” (seeds), przesuwając go w kierunku rozgałęzienia uzyskano przebieg linii prądu widoczny na rysunku 11.

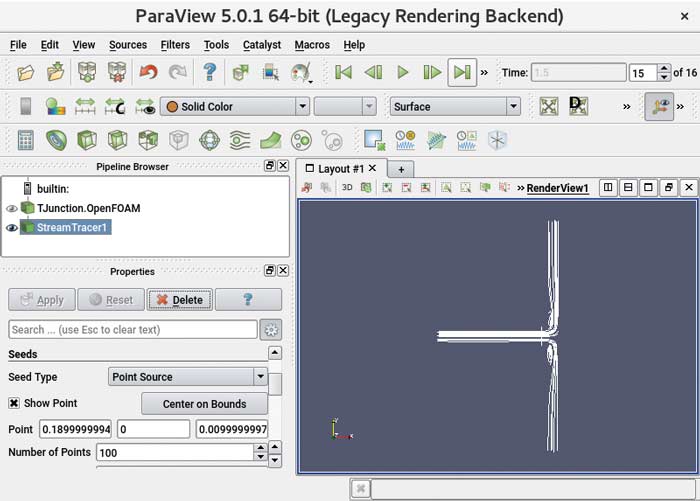
Rys. 11 Linie prądu z uwidocznionymi obszarami zawirowań w rozgałęzieniu

Prezentowane na ekranie wyniki można zapisać w pliku, po wywołaniu z głównej zakładki File polecenia Save Screenshot i zaakceptowaniu proponowanych ustawień przyciskiem Ok (ewentualnie zmieniając rozdzielczość i/lub jakość), a następnie, po podaniu nazwy i typu pliku (standardowo ‘.png’), którego docelowe usytuowanie odczytujemy w górnej części wywołanego okienka (Rys. 12).

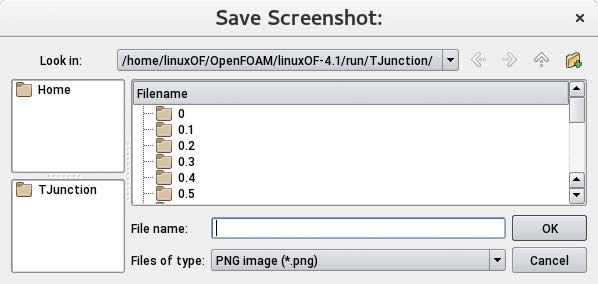
Rys. 12 Okno wyboru nazwy i typu pliku graficznego

Opisana metodologia użytkowania programu graficznego pakietu OpenFOAM umożliwia zilustrowanie przebiegu zmienności pól fizycznych i linii prądu w obszarze obliczeniowym. Pozwala to na dokonanie ogólnej oceny funkcjonowania analizowanego układu przepływowego. Do wykorzystania w pełni potencjału programu graficznego może jednak być potrzebne studium oryginalnych podręczników użytkowania pakietu.

dr inż. Krzysztof Nakonieczny
Ten adres pocztowy jest chroniony przed spamowaniem. Aby go zobaczyć, konieczne jest włączenie w przeglądarce obsługi JavaScript.

Literatura:

1. Launder B.E., Spalding D.B.: Mathematical Models of Turbulence, Academic Press, London, 1972
2. Launder B.E., Spalding D.B.: The numerical computation of turbulent flows, Computer Methods in Applied Mechanics and Engineering, 3/1974
3. Gryboś R.: Podstawy mechaniki płynów, Część 2, Wydawnictwo Naukowe PWN, Warszawa, 1998
4. Issa R.I..: Solution of the implicitly discretised fluid flow equations by operator-splitting, Journal of Computational Physics 62 (1) 1986
5. https://openfoam.org

artykuł pochodzi z wydania 7/8 (130/131) lipiec/sierpień 2018

Czytaj także:

Programy open source do symulacji inżynierskich

Analizy numeryczne DEM transportu elementów sypkich przez układy technologiczne

Modelowanie systemów metodą CFD

Modyfikacja częstotliwości drgań własnych maszyn z wykorzystaniem MES