fwrzesien2018
Jeszcze kilka dekad temu Polska była potentatem w produkcji obrabiarek. Pięćdziesiąt pięć tysięcy produkowanych rocznie maszyn i eksport do trzydziestu krajów świata robi wrażenie i dzisiaj. Wielkie tokarki z Poręby, frezarki z Jarocina czy Pruszkowa i dużo innych obrabiarek polskich producentów są dobrze znane i cenione w wielu krajach świata, także w USA, w których pracują do dzisiaj. Obrabiarki te powstawały wg polskiej dokumentacji i w polskiej technologii. Było to możliwe dzięki planowemu rozwojowi tej branży w naszym kraju. Dzięki temu pojawiło się wiele doskonałych rozwiązań konstrukcyjnych, uświetnionych patentami.
Aleksander Łukomski
Jednym z takich zakładów była słynna fabryka obrabiarek W4 w H. Cegielskim w Poznaniu. Powstała ona początkowo jako fabryka obrabiarek na własne potrzeby holdingu, składającego się z wielu różnych zakładów o różnorodnej produkcji. Szybko jednak okazało się, że obrabiarki te są bardzo dobre i mają wielu klientów spoza H. Cegielskiego. Wiertarki promieniowe WRA, WRB, automaty tokarskie krzywkowe, hydrauliczne, centra tokarskie ze sterowaniem numerycznym i wiele innych, spotyka się i dzisiaj w różnych fabrykach, mimo że W4 już nie istnieje.
W H. Cegielskim obrabiarki nie były najważniejszą produkcją. Na pewno ważniejsze były silniki okrętowe produkowane w dużych ilościach na potrzeby polskiego przemysłu stoczniowego (wtedy – 300 jednostek pływających rocznie), silniki trakcyjne, w tym też do lokomotyw spalinowych, które to lokomotywy i wagony produkowane były na wydziale W3, też w dużych albo bardzo dużych ilościach. Były też dmuchawy, sprężarki, karabiny maszynowe bardzo dobrej jakości i wiele innych znanych wyrobów. W szczytowym okresie rozwoju w H. Cegielskim pracowało dwadzieścia dwa tysiące pracowników. Produkcja polskiego przemysłu maszynowego mieściła się wówczas w wysokich standardach przemysłu światowego i była chętnie kupowana przez różne kraje.
W fabryce W4 działało biuro konstrukcyjne obrabiarek, zatrudniające wielu bardzo zdolnych, a nawet wybitnych konstruktorów. Jednym z nich był długoletni kierownik tego biura – Irakli Zautaszwili. Był on autorem wielu świetnych rozwiązań stosowanych w obrabiarkach. Jednym z takich rozwiązań jest sprzęgło hydrauliczne VHT.

Rys. 1 Ogólny widok sprzęgła VHT z zamontowanym kołem zębatym
Do sterowania sekwencyjnego lub automatycznego (sterownikiem) obrotami wrzeciona i posuwów obrabiarki potrzebny jest mechanizm przełączający mechanicznie zadane odpowiednie przełożenia skrzynki przekładniowej. Trudność polega na tym, że w skrzynce koła zębate i łożyska smarowane są rozbryzgowo olejem, więc nie można zastosować sprzęgieł wielopłytkowych załączanych elektromagnetycznie. Potrzebne było sprzęgło inne, zasilane olejem pod ciśnieniem, poprzez wałek.

Rys. 2 Budowa sprzęgła VHT. 1 – korpus zewnętrzny sprzęgła, 2 – wirnik, 3 – okładzina cierna, 4 – łożyska, 5 – koło zębate, 6 – wpust, X – luz na średnicy, Y – luz pomiędzy membraną a korpusem zewnętrznym, A – otwór doprowadzający olej.
Zautaszwili stworzył takie sprzęgło; zwarte, o stosunkowo prostej budowie, zajmujące mało przestrzeni, napędzane olejem pod ciśnieniem 2,5 MPa. Niepotrzebne są przewody zasilające wewnątrz skrzynki, gdyż zasilanie olejem odbywa się poprzez otwory w wałku. Na korpusie zewnętrznym sprzęgła osadzone jest odpowiednie koło zębate, które gdy sprzęgło nie jest załączone obraca się luźno, a dopiero po załączeniu sprzęgła realizuje się przełożenie przekładni, za pomocą tych kół zębatych, związanych z załączonym sprzęgłem.

Rys. 3 Sprzęgło VHT. Widoczne dwie cienkie stalowe membrany, które pod wpływem oleju podanego pod ciśnieniem poprzez wałek rozchylają się i dociskają do korpusu zewnętrznego, załączając napęd.
Podstawową zaletą sprzęgieł VHT jest mały moment szczątkowy. W VHT wynika on z tarcia tocznego w łożyskach i z oporów resztek oleju w wąskich szczelinach tarczy sprzęgła. Jego wartość, w porównaniu ze sprzęgłami płytkowymi, jest znikoma.
W sprzęgłach płytkowych, osadzonych na pionowych wałkach, głównym oporem jest tarcie między płytkami, wywierane siłą ciężkości oraz ślizgaczami załączenia mechanicznego lub elektrycznego.
Na rysunku 2 widać konstrukcję sprzęgła VHT. Po podaniu oleju pod ciśnieniem do sprzęgła, membrany dociskane są do ścianek korpusu zewnętrznego i następuje zasprzęglenie wałka z przekładnią zębatą, połączoną z tym sprzęgłem.

Rys. 4 Schemat skrzynki przekładniowej z dopuszczalnym rozmieszczeniem sprzęgieł i zasilaniem ich olejem
Po przesterowaniu rozdzielacza podającego olej pod ciśnieniem na to sprzęgło, w pozycję połączoną ze zbiornikiem, zostaje ono rozłączone. Załącza się wtedy inne sprzęgło VHT z innym kołem zębatym i obroty wałka napędzanego są zmienione. Na rysunku 4 pokazano schematycznie dopuszczalną możliwość zamontowania trzech sprzęgieł na jednym wałku.

Rys. 5 Rysunek skrzynki z rozmieszczeniem sprzęgieł VHT i dwoma typami zasilania sprzęgieł olejem: typ A i typ B – zasilanie zewnętrzne. Widoczne kanały w wałkach doprowadzające olej do sprzęgieł.
Możliwość ta zależy przede wszystkim od średnicy wałka i możliwości wywiercenia trzech długich otworów w wałku, dla umożliwienia podania oleju pod ciśnieniem do trzech sprzęgieł; oczywiście każdorazowo tylko do jednego z nich. Powinien być dobrze zaprojektowany schemat hydrauliczny, uniemożliwiający jednoczesne załączenie więcej niż jednego sprzęgła w tej samej skrzynce przekładniowej.
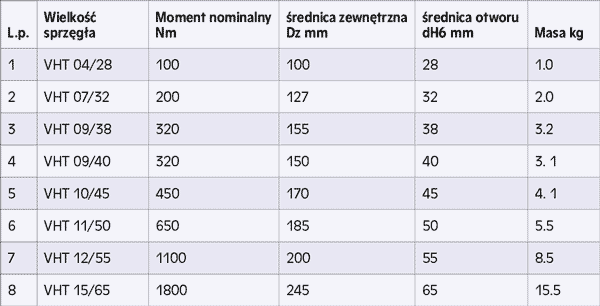
Tab. 1 Typowielkości sprzęgieł VHT
Sprzęgła VHT sprawdziły się w eksploatacji. Są nadal dostępne w handlu, umożliwiają więc tworzenie konstrukcyjne skrzynek przekładniowych, nie tylko obrabiarek, ale i innych maszyn, ze sterowaniem obrotami – sekwencyjnym i automatycznym.
Aleksander Łukomski
artykuł pochodzi z wydania 9 (132) wrzesień 2018
Pininfarina jest ikoną wśród firm tworzących nadwozia samochodowe. W ostatnich latach jednak jej logo coraz rzadziej występuje na produktach wielkich koncernów, które utworzyły własne działy projektowe aby zaoszczędzić na projektach firm zewnętrznych.
Ryszard Romanowski
Mimo utraty wielkoseryjnych kontraktów zarządzana przez Paolo Pininfarinę firma spod turyńskiego Grugliasco cały czas utrzymuje się w awangardzie światowej motoryzacji, prezentując zarówno niepowtarzalny styl, jak i fascynujące rozwiązania techniczne. Warto przypomnieć, że nieżyjący już polski stylista Janusz Kaniewski, który uważał się za „człowieka Pininfariny”, nie lubił gdy nazywano go stylistą. Wolał słowo projektant, ponieważ praca projektanta nie kończyła się na stworzeniu pięknej bryły. Należało jeszcze doskonale znać dostępne rozwiązania techniczne, technologię materiałową i wszystkie zagadnienia niezbędne do z budowania samochodu.

Firma Pininfarina została założona w 1930 roku przez Battistę Pininfarinę, który wcześniej poznał dogłębnie europejski przemysł samochodowy, a w 1920 trafił do zakładów Forda w Detroit. Wspominał, że nie tyle zachwycił go tam system produkcji i rozwiązania techniczne, ile ogromny entuzjazm i otwarcie na nowe, niekonwencjonalne pomysły. Postanowił wrócić do rodzinnego kraju i budować wyróżniające się pod wszystkimi względami samochody. Jego nadwozia wyróżniać zaczęły Alfy Romeo, począwszy od doładowanego modelu 6C. Battista oprócz niezliczonych ilości nagród otrzymał honorowe obywatelstwo kwitnącego wówczas i uznawanego za światową stolicę przemysłu samochodowego, miasta Detroit. Jego następcą na fotelu szefa firmy został w 1961 roku Sergio Pininfarina. Już w roku 1972 na firmowych terenach powstał pełnowymiarowy tunel aerodynamiczny. W tych czasach nie przywiązywali większej wagi do tego urządzenia nawet wielcy, masowi producenci. Warto wspomnieć, że Sergio Pininfarina zasiadał w zarządzie firmy Ferrari w latach 1969-2011. Po jego śmierci w 2012 roku zarządzanie rodzinną firmą przejął syn, Paolo Pininfarina.
U schyłku pierwszej dekady XXI wieku rozpoczęły się gwałtowne zmiany w przemyśle motoryzacyjnym, jak wprowadzenie coraz ostrzejszych norm ekologicznych, wchłanianie mniejszych marek przez wielkie koncerny lub likwidacje wielu producentów, nawet tak zasłużonych, jak Pontiac lub Saab. Z drugiej strony obserwować można coraz większe znaczenie do niedawna niezbyt liczących się krajów azjatyckich, takich jak np. Chiny i Indie. Dalekowschodnie koncerny chętnie wykupują uznane marki, zapewniając im odpowiednie finansowanie. Przykładem może być Volvo, Jaguar i Land Rover. Z drugiej strony chętnie korzystają ze współpracy z europejskimi ośrodkami projektowymi.
cały artykuł dostępny jest w wydaniu 9 (132) wrzesień 2018
Mikrowypraski są elementami występującymi powszechnie w tak wielu urządzeniach i sprzęcie, zarówno codziennego użytku, jak i przemysłowych, że bez nich funkcjonowanie współczesnej gospodarki jak i życie na co dzień byłoby utrudnione. Ich małe wymiary i masa, oraz wąskie tolerancje wymuszają obok stosowania konwencjonalnych metod wtryskiwania, także konieczność korzystania z rozwiązań specjalnych, dedykowanych wyłącznie do wytwarzania mikrowyprasek.
Andrzej Zwierzyński
Mikrowypraski zwykle kojarzone są z małymi wymiarami (rzędu 10-3 mm) i masą (rzędu 0,1 g i mniej). W zasadzie jednak brakuje ich jednoznacznej definicji. Dość dobrze zdefiniowane jest pojęcie mikrowyprasek zaproponowane przez Kunstoff Zentrum (KUZ) Leipzig, gdzie za mikrowypraski uważa się:
wypraski o masie rzędu kilku miligramów i ewentualnie mające wymiary w zakresie mikrometrów, np. mikrokoła zębate, mikrokoszyczki łożysk,
wypraski o wymiarach porównywalnych do tradycyjnych, ale które zawierają obszary (mikrostruktury) z wymiarami w zakresie mikrometrycznym, np. płyty DVD,
wypraski, które mogą mieć większe wymiary, ale mają tolerancje w skali mikrometrycznej, np. mikrozłącza elektryczne czy elementy mechanizmów zegarowych.
Niekiedy błędnie określamy mianem mikrowyprasek wypraski miniaturowe o masie powyżej 0,1 g i nie mające innych wyżej wymienionych cech. Do wytwarzania takich wyprasek można stosować konwencjonalne metody wtrysku, natomiast do wtryskiwania mikrowyprasek wymagane jest obok metod konwencjonalnych sięganie po metody specjalne.
W ostatnich latach rynek całej branży mikrowyprasek należy do najbardziej dynamicznie rozwijających się, z rocznym wzrostem na poziomie ok. 15%, co sprawia, że w okresie od 4 do 5 lat jego wartość ulega podwojeniu. Obecne wysokie zapotrzebowanie na mikrowypraski wzrastało równolegle z systematycznie postępującą miniaturyzacją w elektronice. Wraz z rozwojem technologii mikroprocesorowych przyczyniło się to do zastępowania układów elektromechanicznych miniaturowymi układami elektronicznymi – w różnych dziedzinach. Znaczący wpływ na wzrost zapotrzebowania miał także rozwój w inżynierii materiałowej (nowe tworzywa z grupy HT), technikach wtryskiwania (nowe konstrukcje wtryskarek), urządzeniach peryferyjnych oraz technikach wytwarzania form wtryskowych.

Przykład mikroformy wtryskowej
Obecnie do wytwarzania mikrowyprasek wykorzystywane są głównie termoplasty, ale również duroplasty, elastomery termoplastyczne i ciekłe silikony, oraz metale i ceramika. Dominującą technologią jest wtryskiwanie, tylko w nielicznych przypadkach stosowane jest prasowanie na gorąco i odlewanie podciśnieniowe (Tab. 1). Specyficzne cechy mikrowyprasek oraz stosowanych tworzyw wymuszają stosowanie specjalnych technik wtryskiwania. Do najczęściej wykorzystywanych technik należą: wtryskiwanie wielokomponentowe (zwykle 2K), wytryskiwanie z doprasowaniem, wtryskiwanie duroplastów, wtryskiwanie 3D-MID (Moulded Interconnect Devices), wtryskiwanie ciekłych silikonów oraz wtryskiwanie proszków metali i ceramicznych (tu techniki wtryskiwania są wykorzystywane tylko na pierwszym etapie w całym procesie produkcji wyprasek z tych materiałów).
Największymi obecnie odbiorcami mikrowyprasek są branże: medycyna i ochrona zdrowia (ok. 35%), motoryzacja (ok. 25%), telekomunikacja (ok. 16%) oraz mikronapędy i sterowania (ok. 15%).
cały artykuł dostępny jest w wydaniu 9 (132) wrzesień 2018
(artykuł reklamowy)
Konstruktorzy w różnych branżach wykorzystują łożyska do wielu złożonych i niekonwencjonalnych zastosowań. Dostęp do danych podawanych przez producentów, potwierdzających informacje o wytrzymałości opraw, jest ważnym elementem przy wyborze łożyska, pozwalającym zoptymalizować pracę urządzenia. Jakie kwestie konstrukcyjne należy rozważyć, jeśli zastosowanie wymaga montażu oprawy dzielonej w pozycji innej niż pozioma? Co się dzieje, jeśli obciążenie nie jest przyłożone do podstawy oprawy? Firma Timken odpowiada na te pytania dzięki przeprowadzanym badaniom, zaawansowanej technice modelowania i zdobytemu doświadczeniu. Ułatwia to dobór łożysk do konkretnych zastosowań.
Florin Constantin

Wytrzymałość ma znaczenie
Łożysko to niezwykle ważny element w wielu zastosowaniach przemysłowych. Niezawodność i powtarzalność procesów, w których biorą udział różnego rodzaju łożyska, ma ogromne znaczenie w niezliczonych działaniach zachodzących każdego dnia. W zastosowaniach przemysłowych konstruktorzy zwykle starają się wydłużyć maksymalnie czas pracy maszyn i urządzeń poprzez dobór podzespołów o wysokiej trwałości. W większości zastosowań wykorzystujących łożyska z elementami tocznymi, podstawowymi parametrami służącymi do oszacowania ich trwałości są nośność statyczna i nośność dynamiczna.
Nośność statyczna to maksymalne obciążenie, które łożysko może przenosić bez trwałego uszkodzenia bieżni lub elementów tocznych; oznacza obciążenie przyłożone w stałym, niezmiennym kierunku, w warunkach stacjonarnych.
Nośność dynamiczna to obciążenie promieniowe, przy którym łożyska osiągają trwałość L10, wynoszącą 1 mln obrotów. Wartość obciążenia wykorzystywana jest do szacowania trwałości łożysk w oparciu o rzeczywiste obciążenia i prędkości.
W przypadku opraw dzielonych (znanych także jako zespoły łożyskowe w oprawie), wytrzymałość samej oprawy jest niezwykle istotnym parametrem wpływającym na pracę łożyska – dlatego firma Timken wykonała szereg badań poszczególnych komponentów zespołów łożyskowych pod względem ich wytrzymałości oraz maksymalnych dopuszczalnych obciążeń.
Oprawy niedzielone: Oprawy jednoczęściowe z uszczelnionym i wstępnie nasmarowanym zespołem łożyskowym gotowym do montażu.
Oprawy dzielone: Oprawy dwuczęściowe, z korpusem dzielonym w płaszczyźnie poziomej. Podstawa i pokrywa oprawy są połączone śrubami, co umożliwia łatwiejszy montaż oraz wymianę łożysk i uszczelnień, bez konieczności demontażu podstawy oprawy.
Użytkownicy często korzystają z tego rodzaju rozwiązań w zastosowaniach, w których obciążenia przykładane są w nietypowych kierunkach. W związku z tym często wymagają rozważenia dodatkowych aspektów konstrukcyjnych. Na przykład: jakie należy wprowadzić zmiany konstrukcyjne, jeśli zastosowanie wymaga montażu oprawy dzielonej z podstawą przymocowaną od góry? Jakie rozwiązanie będzie najkorzystniejsze, jeśli obciążenie nie jest przyłożone w kierunku podstawy?
Przy doborze łożysk do danego zastosowania konstruktor bazuje na nośności statycznej oprawy. Dlatego bardzo ważna jest znajomość zakresu wytrzymałości samej oprawy, gdyż pozwala zoptymalizować wydajność pracy urządzenia.
cały artykuł dostępny jest w wydaniu 9 (132) wrzesień 2018
Statyczna próba rozciągania jest podstawową i najbardziej rozpowszechnioną próbą w badaniach własności mechanicznych, która umożliwia wyznaczenie szeregu wskaźników charakteryzujących różnorodne własności materiału, w odniesieniu do zastosowanych parametrów procesu, warunków budowy i procesów wykończeniowych.
Mateusz Oliwa, Aleksander Banaś, Radosław Wojtuszewski
W artykule zaprezentowano metodologię kalibracji parametrów modelu materiałowego Johnsona-Cooka na przykładzie stopu tytanu, wytworzonego w technologii stapiania wiązką elektronów, z wykorzystaniem narzędzi symulacji komputerowej. Celem badań było wyznaczenie podstawowych charakterystyk mechanicznych próbek tytanowych, przeprowadzenie symulacji numerycznej statycznej próby rozciągania próbki oraz znalezienie wartości parametrów modelu materiałowego, tak aby krzywa rozciągania z symulacji korelowała się z krzywą eksperymentalną. Do przeprowadzenia analizy numerycznej wykorzystano solver RADIOSS firmy HyperWorks. W pracy przedstawiono wyniki badań przestrzeni projektowej Design of Experiment optymalizacji i dopasowywania własności materiałowych tytanowej próbki. Dzięki otrzymanym rezultatom można bez obaw stosować model materiałowy w dowolnych symulacjach strukturalnych na prawdziwych konstrukcjach, co pozwala na usprawnienie i optymalizację procesu projektowania poprzez redukcję jego czasu i ograniczenie kosztów.
Statyczna próba rozciągania
Podstawowe charakterystyki mechaniczne próbek wykonanych w technologii EBM zostały wyznaczone w ramach statycznej próby rozciągania, zgodnie z normą PN-EN ISO 6892-1:2009, na maszynie wytrzymałościowej INSTRON 3384 [1, 2].
Do analizy porównawczej wybrane zostały następujące parametry:
- wytrzymałość na rozciąganie Rm
- umowna granica plastyczności Rp0,2
- wydłużenie całkowite A
- moduł Younga E
Charakterystyka próbek
Kształt i wymiary wytworzonych próbek zostały opracowane w oparciu o normę ASTM E8/E8M-11 dla próbek okrągłych, które przedstawiono na rysunku 1.
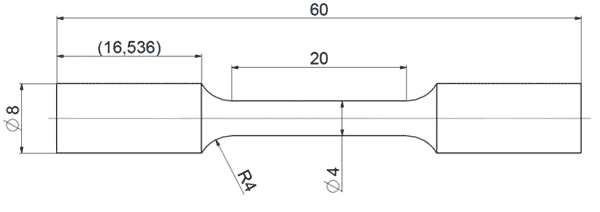
Rys. 1 Kształt i wymiary próbki do próby rozciągania wg ASTM E8/E8M-11
Na rysunku 2 przedstawiono przykład wytworzonej próbki w postaci kształtki, której rozmiar i kształt nadano przy pomocy dodatkowej operacji – obróbki tokarskiej zgodnie z normą ASTME8/E8M-11. Próbki wytworzono z naddatkami 2 [mm], umożliwiającymi wykonanie wykańczającej obróbki mechanicznej, oraz chwytami cylindrycznymi do mocowania w szczękach maszyny wytrzymałościowej.

Rys. 2 Geometria próbki w stanie wyjściowym
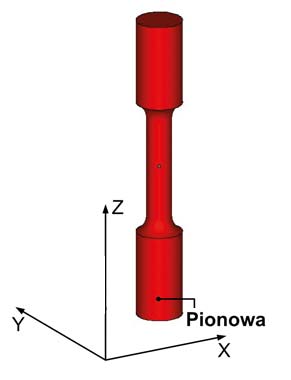
Rys. 3 Kierunek ułożenia na platformie roboczej urządzenia
Testy wykonano na próbkach zorientowanych prostopadle do platformy roboczej w odniesieniu do kierunku budowy „Z”. Orientacja kierunku budowania zgodnie z normą ASTM F2971 – 13.
Opracowanie wyników z prób badawczych
Na rysunku 4 przedstawiono uśredniony wynik statycznych prób wytrzymałościowych, który wykorzystano do symulacji numerycznej.
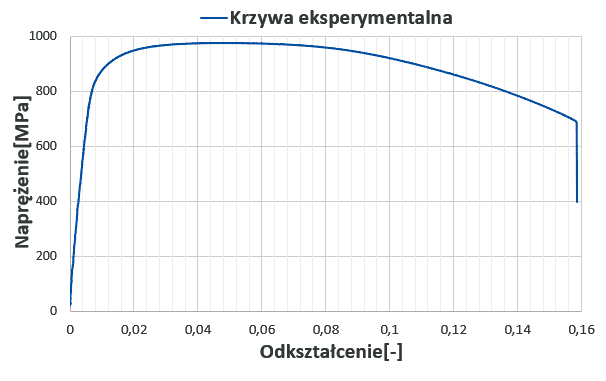
Rys. 4 Uśredniona krzywa eksperymentalna
Budowa modelu obliczeniowego
Na podstawie kształtu i wymiarów próbki wytworzonej ze stopu tytanu zbudowano trójwymiarowy model geometryczny w środowisku CATIA V5. Na rysunku 5 przedstawiono bryłowy model dyskretny, który powstał przez obrót siatki powłokowej względem osi w preprocesorze HyperMesh.

Rys. 5 Model dyskretny próbki
Powstała siatka heksaedryczna daje wysoką dokładność wyników symulacji.
W celu scharakteryzowania prawa materiałowego Johnsona-Cooka potrzebne są trzy główne kroki:
Z krzywej eksperymentalnej odczytanie wartości modułu Younga, granicy plastyczności, wytrzymałości na rozciąganie i odkształcenie przy zerwaniu próbki;
Zamiana naprężeń i odkształceń inżynierskich na wartości rzeczywiste przy wykorzystaniu poniższych zależności 1.1 oraz 1.2;
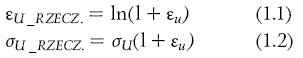
Obliczenie parametrów Johnsona- Cooka tj. moduł umocnienia oraz wykładnik umocnienia, które definiują plastyczną część krzywej. Wzory 1.3 [3] oraz 1.4 [3] odpowiednio określają te parametry.
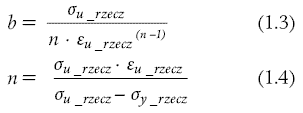
W celu zamodelowania uchwytów klinowych, zadano utwierdzenie uniemożliwiające przemieszczenie we wszystkich kierunkach i rotację wokół wszystkich osi próbki na jednym końcu. Na drugim końcu przyłożono rozciąganie poprzez wymuszoną prędkość. Model numeryczny z zadanymi obciążeniami i utwierdzeniem przedstawiono na rysunku 6.
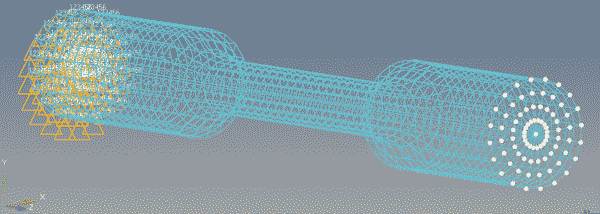
Rys. 6 Model numeryczny z warunkami brzegowymi
W celu pozyskania sił w bazie wyników, stworzono tzw. sekcję w połowie długości próbki, zaś dla zachowania przemieszczeń zdefiniowano pewien węzeł na końcu próbki. Na rysunkach 7 i 8 przedstawiono model z określonymi – sekcją oraz węzłem.
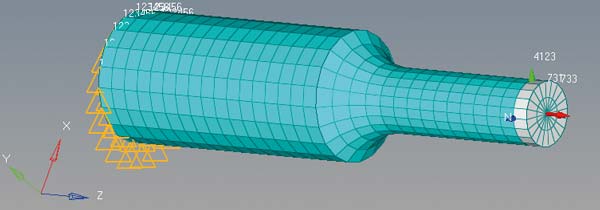
Rys. 7 Model numeryczny ze zdefiniowaną sekcją
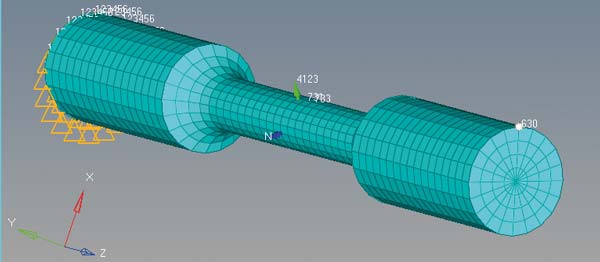
Rys. 8 Model numeryczny ze zdefiniowanym węzłem
Z wyników symulacji odczytano zmienność siły i przemieszczenia (Rys. 9), które należało przekonwertować odpowiednio na naprężenia i odkształcenia, gdyż tylko wtedy można byłoby przeprowadzić ilościowe porównanie z eksperymentem.
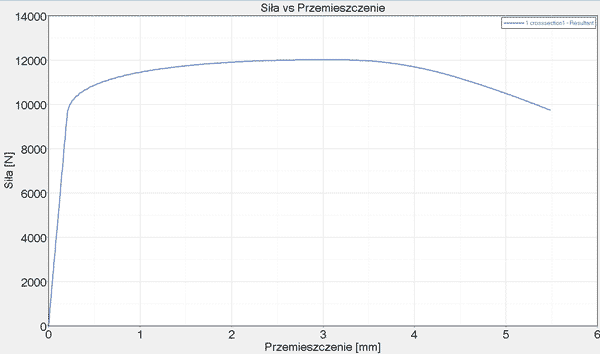
Rys. 9 Krzywa rozciągania przed konwersją
Naprężenia inżynierskie uzyskuje się poprzez podzielenie siły przez początkowy przekrój, zaś odkształcenia inżynierskie – poprzez podzielenie przemieszczenia zdefiniowanego węzła na drugim końcu przez długość próbki. Porównanie krzywej eksperymentalnej i wykresu Johnsona-Cooka po konwersji przedstawiono na rysunku 10.

Rys. 10 Porównanie krzywej eksperymentalnej oraz krzywej Johnsona-Cooka
Wyniki obliczeń
W wyniku przeprowadzenia analizy nieliniowej otrzymano obliczenie słabo skorelowane z eksperymentem. Model numeryczny próbki jest zbyt sztywny i osiąga mniejsze wartości naprężeń powyżej granicy plastyczności dla danych wartości odkształceń. Rozbieżność jest znaczna. Punkt przewężenia dla obu krzywych jest w podobnym zakresie.
HyperStudy do badania przestrzeni projektowej
Badanie przestrzeni projektowej (Design of Experiment) daje nam wskazówki na temat wpływu poszczególnych zmiennych na interesujące nas cechy. Pozwala uświadomić jakie są relacje między charakterystyką krzywej rozciągania, a zmiennymi projektowymi tj. moduł Younga, granica plastyczności, moduł umocnienia i wykładnik umocnienia. Dzięki temu można zweryfikować, w jakim stopniu parametry mają wpływ na zmienność charakterystyki naprężnie-odkształcenie.
W celu korelacji krzywej z symulacji i eksperymentu wybrano cztery punkty kontrolne, dla których narzędzie Hyperstudy i jego pełny algorytm czynnikowy (full factorial method) przyrównuje obie te krzywe. Algorytm ten szacuje wszelkie możliwe kombinacje wprowadzonych zmiennych. Wystarczy tylko podać pewien zakres szukanych wartości.
Zdefiniowanie punktów kontrolnych, które zaznaczono graficznie na rysunku 10, odbywa się za pomocą pewnych funkcji, które są wbudowane w panelu tworzenia wyrażeń (Expression Builder). Zawiera on listę matematycznych rozwiązań, które można wybrać, aby określić własności jakie chcemy osiągnąć.

Rys. 11 Metody badawcze przestrzeni projektowej
Na rysunku 12 przedstawiono wprowadzone interpolacje funkcji liniowej do obliczenia naprężeń dla 2- i 3-procentowego odkształcenia. W celu znalezienia maksymalnego naprężenia i odkształcenia, w punkcie przewężenia dla charakterystyki rozciągania, posłużono się maximum funkcji.

Rys. 12 Funkcje matematyczne Expression Builder
Wyniki obliczeń przestrzeni projektowej
Do oceny poszczególnych zmiennych najczęściej wykorzystywany jest diagram Pareto. Celem jest pokazanie najbardziej istotnych spośród dużej liczby czynników. Pojedyncze wartości parametrów reprezentowane są przez słupki w porządku malejącym. Na jej podstawie jesteśmy w stanie wskazać, które wprowadzone zmienne są istotne dla optymalizacji krzywej Johnsona-Cooka, a które należy zaniedbać. Na rysunku 13 wykres wskazuje, że moduł Younga ma znaczący wpływ na wprowadzony punkt kontrolny.
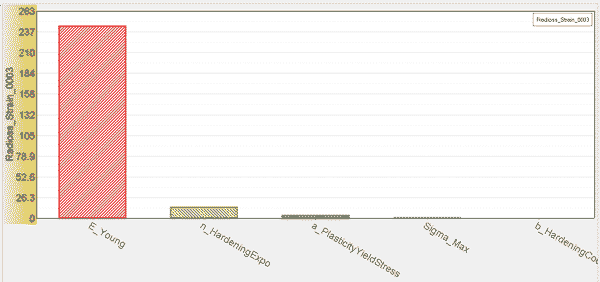
Rys. 13 Wykres Pareto dla sprężystej charakterystyki krzywej
To ma sens, z racji tego, że ten parametr wpływa na cześć sprężystą krzywej, gdzie zaistniały największe różnice. Influencja maksymalnego naprężenia jest nieistotna, ponieważ odnosi się do punktu kontrolnego powyżej puntu przewężenia, którego wybrane prawo materiałowe nie bierze pod uwagę. Rozważając te badania można dojść do wniosku, że bezpiecznie będzie pominąć ten parametr w przypadku optymalizacji.
Kalibracja materiału
Kolejny etapem będzie dopasowanie parametrów modelu materiałowego Johnsona-Cooka przy wykorzystaniu specjalnego narzędzia System Identification. Ten typ rozwiązania dąży do zmniejszenia sumy kwadratu błędu tj. różnicy między obliczeniem numerycznym a zadaną wartością docelową. Warto zauważyć, że przy tym rodzaju optymalizacji nie wprowadzamy żadnych równań czy funkcji ręcznie, lecz jednoznacznie wstawiamy pożądane wartości dla każdej odpowiedzi [6].
Ważnym aspektem jest także dobór metody optymalizacji opartej na aproksymacji. W zagadnieniu tym zbieżność rozwiązania można uzyskać dzięki zastosowaniu podejścia Global Response Surface Method, którą przedstawiono na rysunku 14.

Rys. 14 Zestawienie metod aproksymacji optymalizacji
Powierzchnia odpowiedzi jest adaptacyjnie aktualizowana poprzez nowe rozwiązania, by znaleźć lepsze dopasowanie modelu. Świetnie się nadaje do zagadnień związanych z kilkoma celami lub gdy zdefiniowanych jest wiele zmiennych projektowych. Jeśli analiza modelu jest czasochłonna, wtedy ta metoda jest dobrym rozwiązaniem. Dla krótkich analiz i dokładnych poszukiwań przestrzeni projektowej zaleca się podejście Genetic Algorithm lub Multi-Objective Genetic Algorithm [4, 5].
Wyniki i wnioski obliczeń optymalizacji
W wyniku optymalizacji uzyskano zadowalającą zbieżność w zakresie 1%. Na rysunku 15 łatwo zauważyć znaczącą różnicę przed i po optymalizacji. Charakterystyka modelu materiału dla próbki tytanu bardzo dobrze się koreluje z krzywą eksperymentalną.
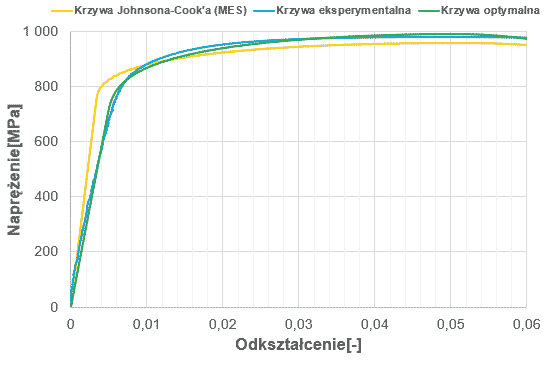
Rys. 15 Porównanie eksperymentu, krzywej Johnsona-Cooka przed i po optymalizacji
Wykorzystując badanie przestrzeni projektowej oraz optymalizację zamiast podejścia metodą prób i błędów, która jest tradycyjnym sposobem wykonywania kalibracji modelu, można zmniejszyć czas na kalibrację i zwiększyć jej jakość. Program HyperStudy ma specjalne metody optymalizacyjne, takie jak System Identification, w celu przyspieszenia procesu przygotowania symulacji.
Mateusz Oliwa
Ten adres pocztowy jest chroniony przed spamowaniem. Aby go zobaczyć, konieczne jest włączenie w przeglądarce obsługi JavaScript.
Aleksander Banaś
Ten adres pocztowy jest chroniony przed spamowaniem. Aby go zobaczyć, konieczne jest włączenie w przeglądarce obsługi JavaScript.
Radosław Wojtuszewski
Ten adres pocztowy jest chroniony przed spamowaniem. Aby go zobaczyć, konieczne jest włączenie w przeglądarce obsługi JavaScript.
Sekcja Techniczna Projektu Technologii Przyrostowych
PZL Mielec A Sikorsky Company
Literatura:
Beluch W., Burczyński T., Fedeliński P., John A., Kokot G., Kuś W. „Laboratorium z wytrzymałości materiałów”. Gliwice: Wydawnictwo Politechniki Śląskiej, 2002
Konowalski K. Statyczna próba rozciągania metali. Szczecin: Wydział Inżynierii Mechanicznej i Mechatroniki, Szczecin, 2015
Altair HyperWorks, Introduction to RADIOSS for Impact, Chapter 5: Material Laws and Characterization, 2016
https://altairhyperworks.com/hwhelp/Altair/2017/help/hst/hst.htm?hs_4200.htm
Altair HyperWorks, „HyperStudy” Altair Engineering, 2009
Kocer-Poyraz F. „Model Calibration Using Optimization Techniques”. Altair HyperWorks, 2012
artykuł pochodzi z wydania 9 (132) wrzesień 2018
Specjalistyczny portal inżynierski dla osób zaangażowanych w tworzenie produktów – maszyn, urządzeń, mechanizmów, podzespołów, części, elementów itd. – od koncepcji do ostatecznego wykonania.






