Statyczna próba rozciągania jest podstawową i najbardziej rozpowszechnioną próbą w badaniach własności mechanicznych, która umożliwia wyznaczenie szeregu wskaźników charakteryzujących różnorodne własności materiału, w odniesieniu do zastosowanych parametrów procesu, warunków budowy i procesów wykończeniowych.

Mateusz Oliwa, Aleksander Banaś, Radosław Wojtuszewski

W artykule zaprezentowano metodologię kalibracji parametrów modelu materiałowego Johnsona-Cooka na przykładzie stopu tytanu, wytworzonego w technologii stapiania wiązką elektronów, z wykorzystaniem narzędzi symulacji komputerowej. Celem badań było wyznaczenie podstawowych charakterystyk mechanicznych próbek tytanowych, przeprowadzenie symulacji numerycznej statycznej próby rozciągania próbki oraz znalezienie wartości parametrów modelu materiałowego, tak aby krzywa rozciągania z symulacji korelowała się z krzywą eksperymentalną. Do przeprowadzenia analizy numerycznej wykorzystano solver RADIOSS firmy HyperWorks. W pracy przedstawiono wyniki badań przestrzeni projektowej Design of Experiment optymalizacji i dopasowywania własności materiałowych tytanowej próbki. Dzięki otrzymanym rezultatom można bez obaw stosować model materiałowy w dowolnych symulacjach strukturalnych na prawdziwych konstrukcjach, co pozwala na usprawnienie i optymalizację procesu projektowania poprzez redukcję jego czasu i ograniczenie kosztów.
Statyczna próba rozciągania
Podstawowe charakterystyki mechaniczne próbek wykonanych w technologii EBM zostały wyznaczone w ramach statycznej próby rozciągania, zgodnie z normą PN-EN ISO 6892-1:2009, na maszynie wytrzymałościowej INSTRON 3384 [1, 2].
Do analizy porównawczej wybrane zostały następujące parametry:

• wytrzymałość na rozciąganie R_m
• umowna granica plastyczności R_p0,2
• wydłużenie całkowite A
• moduł Younga E

Charakterystyka próbek
Kształt i wymiary wytworzonych próbek zostały opracowane w oparciu o normę ASTM E8/E8M-11 dla próbek okrągłych, które przedstawiono na rysunku 1.

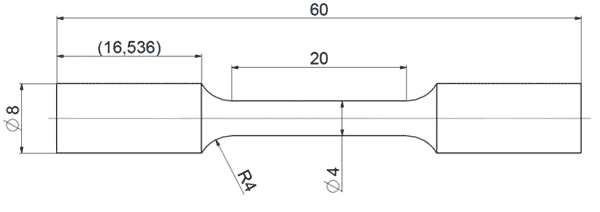
Rys. 1 Kształt i wymiary próbki do próby rozciągania wg ASTM E8/E8M-11

Na rysunku 2 przedstawiono przykład wytworzonej próbki w postaci kształtki, której rozmiar i kształt nadano przy pomocy dodatkowej operacji – obróbki tokarskiej zgodnie z normą ASTME8/E8M-11. Próbki wytworzono z naddatkami 2 [mm], umożliwiającymi wykonanie wykańczającej obróbki mechanicznej, oraz chwytami cylindrycznymi do mocowania w szczękach maszyny wytrzymałościowej.

Rys. 2 Geometria próbki w stanie wyjściowym

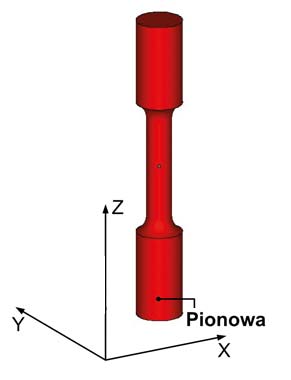
Rys. 3 Kierunek ułożenia na platformie roboczej urządzenia

Testy wykonano na próbkach zorientowanych prostopadle do platformy roboczej w odniesieniu do kierunku budowy „Z”. Orientacja kierunku budowania zgodnie z normą ASTM F2971 – 13.

Opracowanie wyników z prób badawczych
Na rysunku 4 przedstawiono uśredniony wynik statycznych prób wytrzymałościowych, który wykorzystano do symulacji numerycznej.

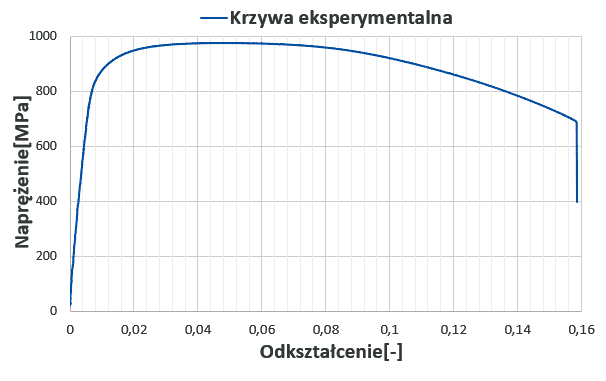
Rys. 4 Uśredniona krzywa eksperymentalna

Budowa modelu obliczeniowego
Na podstawie kształtu i wymiarów próbki wytworzonej ze stopu tytanu zbudowano trójwymiarowy model geometryczny w środowisku CATIA V5. Na rysunku 5 przedstawiono bryłowy model dyskretny, który powstał przez obrót siatki powłokowej względem osi w preprocesorze HyperMesh.

Rys. 5 Model dyskretny próbki

Powstała siatka heksaedryczna daje wysoką dokładność wyników symulacji.
W celu scharakteryzowania prawa materiałowego Johnsona-Cooka potrzebne są trzy główne kroki:
Z krzywej eksperymentalnej odczytanie wartości modułu Younga, granicy plastyczności, wytrzymałości na rozciąganie i odkształcenie przy zerwaniu próbki;
Zamiana naprężeń i odkształceń inżynierskich na wartości rzeczywiste przy wykorzystaniu poniższych zależności 1.1 oraz 1.2;

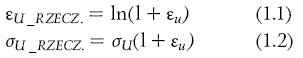
Obliczenie parametrów Johnsona- Cooka tj. moduł umocnienia oraz wykładnik umocnienia, które definiują plastyczną część krzywej. Wzory 1.3 [3] oraz 1.4 [3] odpowiednio określają te parametry.

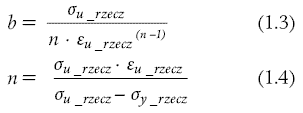
W celu zamodelowania uchwytów klinowych, zadano utwierdzenie uniemożliwiające przemieszczenie we wszystkich kierunkach i rotację wokół wszystkich osi próbki na jednym końcu. Na drugim końcu przyłożono rozciąganie poprzez wymuszoną prędkość. Model numeryczny z zadanymi obciążeniami i utwierdzeniem przedstawiono na rysunku 6.

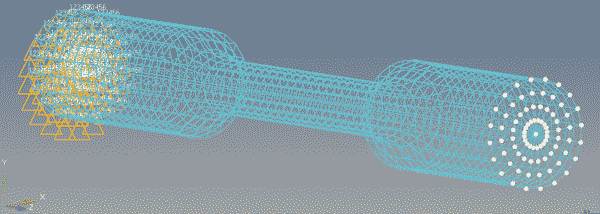
Rys. 6 Model numeryczny z warunkami brzegowymi

W celu pozyskania sił w bazie wyników, stworzono tzw. sekcję w połowie długości próbki, zaś dla zachowania przemieszczeń zdefiniowano pewien węzeł na końcu próbki. Na rysunkach 7 i 8 przedstawiono model z określonymi – sekcją oraz węzłem.

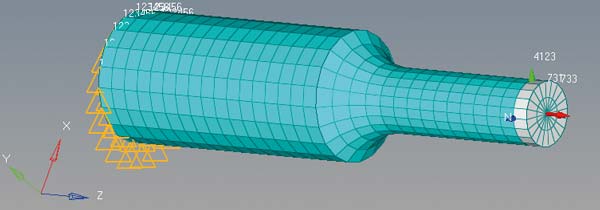
Rys. 7 Model numeryczny ze zdefiniowaną sekcją

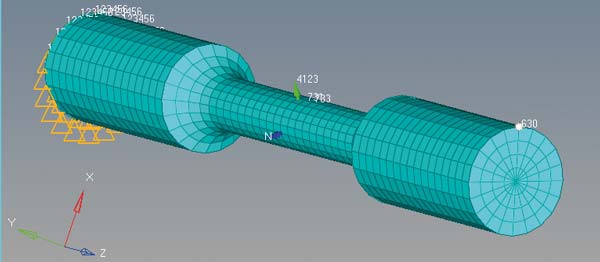
Rys. 8 Model numeryczny ze zdefiniowanym węzłem

Z wyników symulacji odczytano zmienność siły i przemieszczenia (Rys. 9), które należało przekonwertować odpowiednio na naprężenia i odkształcenia, gdyż tylko wtedy można byłoby przeprowadzić ilościowe porównanie z eksperymentem.

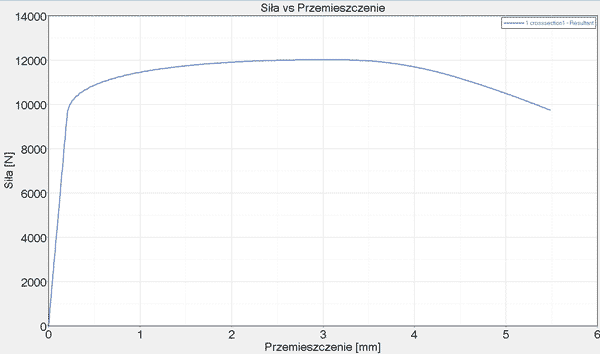
Rys. 9 Krzywa rozciągania przed konwersją

Naprężenia inżynierskie uzyskuje się poprzez podzielenie siły przez początkowy przekrój, zaś odkształcenia inżynierskie – poprzez podzielenie przemieszczenia zdefiniowanego węzła na drugim końcu przez długość próbki. Porównanie krzywej eksperymentalnej i wykresu Johnsona-Cooka po konwersji przedstawiono na rysunku 10.

Rys. 10 Porównanie krzywej eksperymentalnej oraz krzywej Johnsona-Cooka