Zespół cech pojazdów odpowiadających za bezpieczeństwo pasażerów w trakcie kolizji określa się mianem bezpieczeństwa biernego. Dla porównania, cechy pojazdu, które zapobiegają kolizji, odpowiadają za tzw. bezpieczeństwo czynne. Klasyczna koncepcja systemu bezpieczeństwa biernego wykorzystuje ideę sztywnej klatki otoczonej deformowanymi elementami pochłaniającymi energię zderzenia.

Marian Ostrowski, Piotr Bartkowski, Bartłomiej Błaszczak, Jakub Skomoroko

Takie działanie konstrukcji jest zauważalne szczególnie w przypadku zderzeń przednich bądź tylnych. Koncept ten jest nieco rozmyty w przypadku zderzeń bocznych, gdzie mała ilość miejsca utrudnia możliwość odseparowania roli absorbera i sztywnej klatki bezpieczeństwa. Zgniatanie absorberów powoduje obciążenie klatki bezpieczeństwa oraz pasażerów polem przyspieszeń.

Rys. 1  Model zderzenia pojazdu wyposażonego w elementy bezpieczeństwa biernego

Kluczową rolę w minimalizowaniu negatywnych skutków przyspieszeń odgrywają systemy wnętrza pojazdu, takie jak: fotele, pasy bezpieczeństwa czy poduszki gazowe. W niniejszym artykule opisano sposób projektowania i badań numerycznych konstrukcji pojazdów odpornych na zderzenia. Dodatkowo w pracy przedstawiono tematykę modelowania poduszek gazowych.

Projektowanie struktur odpornych na zderzenia
W firmie Invenco rozwinięto unikatowe metody projektowania strefy zderzeniowych oraz  struktur nośnych pojazdów. Do tego celu są wykorzystywane rozwiązania będące połączeniem klasycznych technik analitycznych z metodą elementów skończonych, stopniowo podnosząc stopień złożoności modeli, uwzględniających wszystkie istotne cechy konstrukcji, takie jak: sztywność, wytrzymałość, nośność, kinematyka deformacji czy energochłonność.

Rys. 2  Schemat postępowania przy projektowaniu stref zderzeniowych

Pierwszą fazą projektu jest wykonanie obliczeń związanych ze wstępnym doborem parametrów strefy zderzeniowej. Na podstawie bilansu energii zderzenia, średnich opóźnień i cech geometrycznych dobiera się wstępną charakterystykę strefy energochłonnej dla każdego ze scenariuszy zderzeniowych. W następnym kroku przygotowywane są proste modele numeryczne, które dają możliwość określenia kinematyki mechanizmów plastycznych. Modele bazujące na elementach jednowymiarowych pozwalają również na określenie przybliżonych poziomów sił i energochłonności danego elementu konstrukcyjnego. W kolejnym kroku następuje projektowanie przekrojów, na podstawie dobranych sił średnich, za pomocą wzorów analitycznych i stworzonych specjalnie do tego arkuszy kalkulacyjnych. W celu uzyskania jak najlepszej efektywności przekroju używane są procedury optymalizacyjne bazujące na podstawach numeryczno-analitycznych. W tej fazie również znajdują zastosowanie narzędzia do badania przestrzeni rozwiązań, takie jak Ls-Opt. Umożliwiają one zbadanie wrażliwości układu na zmienność parametrów, określenie obszarów globalnej stateczności i niestateczności, czy też wielokryterialną optymalizację wybranych cech konstrukcyjnych.
Po wstępnym dobraniu przekrojów przygotowywane są modele MES wyższego rzędu, bazujące na elementach dwu- i trójwymiarowych. Modele te pozwalają na zwiększanie stopnia złożoności układu, umożliwiając uwzględnienie zjawisk lokalnych, które nie zostały właściwie oddane we wstępnej fazie projektu. Równolegle są uwzględniane w procesie inżynierskim pozostałe, zwykle niewymiarujące globalnie cechy, związane z wytrzymałością na obciążenia eksploatacyjne.
Etap modelu szczegółowego umożliwia wprowadzenie precyzyjnego modelu przyrządu pomiarowego w postaci manekina antropometrycznego. W symulacjach przedstawionych w artykule użyto uproszczonego modelu ATD typu HYBRID III, którego poziom dokładności jest wystarczający do wstępnej oceny układu. Wraz z wprowadzeniem modelu manekina możliwe staje się uwzględnienie istotnych cech systemu więzów wewnętrznych, takich jak fotel, pasy bezpieczeństwa czy poduszki gazowe. Stanowią one kolejny, wewnętrzny system absorberów energii zderzenia, bezpośrednio wpływając na stosunkowo skomplikowane zachowanie się manekina pomiarowego. Zadanie inżynierskie polega na zapewnieniu nieprzekraczania uznawanych za krytyczne wartości parametrów biomechanicznych, wśród których znajdują się między innymi: indeks obrażeń głowy (HIC – head injury criteria), głębokość wgniecenia modelu klatki piersiowej czy też siła osiowa w kości udowej.

Projektowanie poduszek gazowych
Na przestrzeni ostatnich trzydziestu lat algorytmy obliczeniowe do symulacji zachowania poduszek w komercyjnych programach MES uległy znacznej ewolucji. Początkowo stosowano model bazujący na jednorodnym ciśnieniu wewnętrznym, którego ewolucja była określana zgodnie z równaniem stanu gazu idealnego. Tak określone ciśnienie przykładano do wewnętrznych powierzchni elementów powłokowych modelujących zachowanie tkaniny, co pozwalało na dobre określenie zachowania poduszki w stanie rozłożonym, przy relatywnie niskich prędkościach deformacji.

Rys. 3  Badana próbka materiału wraz z mapą odkształceń

Powyższy model nie pozwala jednak na opisanie z wystarczającą dokładnością procesu rozkładania poduszki, gdzie z inflatora wydostaje się gaz z dużą energią kinetyczną, formując quasi-stożkowy strumień, który znacząco zmienia efektywny rozkład ciśnień. Pośrednio dobre wyniki dla procesu rozkładania osiągano stosując modele heurystyczne, dodające składową od strumienia w obszarze stożka określonego na podstawie oddzielnych badań. Rozwój wymagań związanych z symulacją oddziaływania poduszek na użytkowników będących w obszarze rozkładu wymusił zastosowanie bardziej zaawansowanych metod, takich jak modele wykorzystujące opis Eulerowski bądź ALE, lub metod cząsteczkowo-stochastycznych CPM.

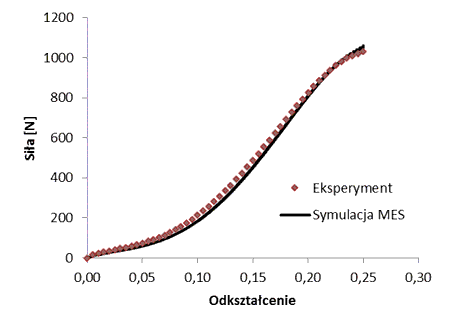
Rys. 4  Charakterystyka rozciągania  tkaniny poduszki gazowej – porównanie wyników eksperymentalnych i symulacyjnych

Aby prawidłowo projektować poduszki gazowe badania symulacyjne muszą być korelowane z badaniami eksperymentalnymi. Tkaniny, z których zwykle produkowane są poduszki, charakteryzują się silnie nieliniowymi własnościami mechanicznymi oraz ortotropią, w związku z czym numeryczne przewidywanie ich zachowania w zakresie dużych deformacji jest znacznie trudniejsze niż klasycznych izotropowych sprężysto-plastycznych materiałów inżynierskich. Do określenia wytężenia konstrukcji ze stali czy aluminium bardzo często wystarcza literaturowa znajomość podstawowych danych materiałowych, takich jak: moduł Younga i liczba Poissona oraz granica plastyczności.