Podczas procesu projektowania urządzeń oraz maszyn najważniejszym celem jest spełnienie podstawowych założeń projektowych, takich jak funkcjonalność produktu, odpowiednia wytrzymałość mechaniczna czy ciekawy i wyróżniający się design. Jednak zdecydowana większość projektów ma więcej wymagań, których spełnienie jest bardzo zasobo- oraz czasochłonne.
Maciej Majerczak
Przy rozwiązywaniu tego typu problemów efektywne może być zastosowanie komputerów, w celu znalezienia optymalnego rozwiązania. Maszyny są w stanie w krótkim czasie sprawdzić wiele różnorodnych designów i wytypować te najbardziej obiecujące. W zależności od poszukiwanych rozwiązań, można zastosować na przykład metodę DOE (Design of Experiment), kiedy to przy pomocy algorytmów staramy się przedstawić zależności pomiędzy parametrami i ich wpływem na wynik finalny. Innym, bardzo ciekawym sposobem optymalizacji konstrukcji, jest optymalizacja bazująca wprost na geometrii CAD. Do tego typu analiz można zaliczyć między innymi optymalizację topologiczną i topograficzną.
Niestety niejednokrotnie analizowane przez nas problemy z racji swej złożoności wymagają dużych mocy obliczeniowych, co znacząco wpływa na wydłużenie czasu obliczeń. Często również, projektowany komponent jest częścią większego złożenia i przygotowanie takiej analizy bez uwzględnienia otoczenia byłoby zbyt dużym uproszczeniem, a co za tym idzie, mogłoby to doprowadzić do poważnego błędu projektowego. Dlatego w takich przypadkach zastosowanie znajdują substruktury (tzw. superelementy), za pomocą których przedstawia się reprezentację zastępczą otoczenia.
Artykuł ten jest kontynuacją wcześniejszej publikacji (z maja br.), w której przedstawiono główne idee wykorzystania tego typu struktur w obliczeniach MES.
Optymalizacja konstrukcji przy użyciu MES
Optymalizację konstrukcji z wykorzystaniem metody elementów skończonych przeprowadza się w celu znalezienia najlepszego możliwego rozwiązania dla danego problemu inżynierskiego. Analiza optymalizacyjna musi składać się z wszystkich podstawowych danych potrzebnych do przeprowadzenia obliczeń numerycznych, takich jak:
- siatka elementów skończonych reprezentująca analizowaną geometrię,
- podstawowe dane materiałowe takie jak moduł Younga, liczba Poissona czy gęstość materiału dla analiz dynamicznych,
- warunki brzegowe, takie jak na przykład utwierdzenia,
- wymuszenie, np. siłą lub przemieszczeniem.
Niektóre typy analiz nie wymagają warunków brzegowych oraz klasycznie rozumianego wymuszenia. Jest to między innymi analiza modalna, dla której również możliwe jest przeprowadzenie optymalizacji. Celem w tego typu optymalizacji może być między innymi przesunięcie częstotliwości własnych poprzez zmianę masy lub sztywności konstrukcji.
Należy również zauważyć, że podczas analizy optymalizacji przeprowadzane obliczenia mają charakter iteracyjny.

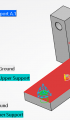
Rys. 1 Przykładowy wynik uzyskany przy pomocy optymalizacji topologicznej
padtinc.com/blog/additive-manufacturing-back-to-the-future/
Oznacza to, że będą one wielokrotnie powtarzane, aż do momentu uzyskania zadowalającego nas efektu. Ze względu na iteracyjność metody, zalecane jest przygotowywanie modeli, których jedna pętla obliczeniowa trwa stosunkowo krótko. Aby to osiągnąć najłatwiej jest uprościć model do akceptowalnego przez nas minimum, poprzez zmniejszenie ilości elementów lub uproszczenie skomplikowanych złożeń. Inną drogą jest zastosowanie metody substruktur, za pomocą której zastąpić można elementy konstrukcji mające wpływ na zachowanie całego złożenia. Należy jednak pamiętać, że takie uproszczenie spowoduje utratę szczegółowych wyników dla upraszczanych komponentów.
cały artykuł dostępny jest w wydaniu 10 (145) październik 2019