W środowisku programistycznym mówi się, że aby zrozumieć rekurencję należy najpierw zrozumieć czym jest rekurencja. Podobnej analogii można użyć, aby określić czym jest optymalizacja; chcąc zrozumieć czym ona jest należy najpierw zrozumieć co oznacza przymiotnik optymalny. Słownik PWN określa optymalny jako najlepszy z możliwych w jakichś warunkach. Bardzo wyraźnie podkreślony jest tu fakt, że bycie „najlepszym” zależy od warunków zewnętrznych, a te zależą od sytuacji, którą rozpatrujemy. Przykładowo, samochód marki Porsche na pewno nie będzie wyborem optymalnym dla osoby szukającej swojego pierwszego samochodu. W tym przypadku głównym warunkiem zewnętrznym ograniczającym nasz wybór jest oczywiście budżet. Wiedząc co oznacza przymiotnik optymalny łatwo zdefiniować czym jest optymalizacja. Jest to proces polegający na udoskonaleniu jakiegoś obiektu czy procesu, tak aby posiadał możliwie najlepsze cechy w z góry określonych warunkach. Warto też podkreślić, że proces udoskonalenia może polegać zarówno na maksymalizacji jak i minimalizacji wpływu jakieś cechy.
Sławomir Polański
Podstawy optymalizacji matematycznej
W historii nauk technicznych znaleźć można wiele przypadków rywalizacji między naukowcami. Jednym z przykładów są bracia Johann i Jakob Bernoulli. Źródła podają, że młodszy z braci, Johann, zazdrościł stanowiska profesorskiego swojemu starszemu bratu, co wytworzyło nić rywalizacji między nimi. Całe szczęście dla nauki, rywalizacja ta była przyczynkiem do rozwoju matematyki, a w szczególności analizy matematycznej. W roku 1696 Johann rzucił wyzwanie całemu matematycznemu światu w postaci matematycznej zagwozdki, która brzmiała mniej więcej tak: mając do dyspozycji punkty A i B wyznacz równanie krzywej, po której masa punktowa pod wpływem siły ciężkości stacza się w możliwie najkrótszym czasie. Ten matematyczny problem nazywany jest dziś zagadnieniem krzywej najkrótszego spadku bądź zagadnieniem brachistochrony (od nazwy krzywej). Można powiedzieć, że jest to w sumie pytanie o to, jaki kształt powinna mieć skocznia narciarska, tak by skoczkowie zjechali po niej w jak najszybszym czasie. Ciekawostką jest, że za rozwiązanie zagadki Johann zaoferował nagrodę i jednocześnie sam zaproponował rozwiązanie w postaci równania cykloidy. W późniejszym czasie starszy brat Jakob udowodnił, że równanie cykloidy jest w istocie rozwiązaniem problemu, ale sposób w jaki chciał to udowodnić Johann był niepoprawny.
Bracia Bernoulli stworzyli podwaliny rachunku wariacyjnego. Jednym z głównych zadań tej dziedziny matematyki jest znalezienie odpowiedzi na każde pytanie zaczynające się od słów „oblicz najlepszy / maksymalny / minimalny / najdłuższy / najkrótszy...” itp. Brzmi znajomo? Powinno. Rachunek wariacyjny to w istocie narzędzie matematyczne służące do przeprowadzania optymalizacji. Wykorzystuje się go do badania ekstremalnych wartości funkcji, które w rachunku wariacyjnym nazywane są funkcjami celu.
Piękno matematyki polega na tym, że często to samo rozwiązanie można otrzymać kilkoma sposobami. Z tego właśnie powodu postanowiłem sprawdzić czy problem krzywej najkrótszego spadku da się rozwiązać przy użyciu dostępnych narzędzi do symulacji inżynierskich. Zakładając, że mamy do dyspozycji masę punktową oraz krzywą przechodzącą przez trzy punkty, symulacja zostanie wykorzystana by określić całkowity czas potrzebny na pokonanie krzywej przez masę punktową. W takim przypadku funkcją celu będzie wspomniany czas, a jej wartością możemy manipulować poprzez dobranie odpowiednich wartości A, B i C (Rys. 1).

Rys. 1 Wstępny szkic krzywej najkrótszego spadku
Jak to zrobić? Można ręcznie manipulować wartościami i sprawdzać, które proporcje wymiarów skracają czas potrzebny na pokonanie krzywej. Innym podejściem jest wykorzystanie algorytmów optymalizacyjnych, które same dobierają odpowiednie wartości wymiarów tak, aby kierunek zmian był najbardziej pożądany.

Rys. 2 Poszczególne klatki z wideo przedstawiającego w jaki sposób algorytm optymalizacyjny dobiera proporcje wymiarów A, B, C tak aby czas spadku był najmniejszy
Przykład z rysunku 2 to chyba najprostszy możliwy przykład optymalizacji z wykorzystaniem oprogramowania komputerowego. Podobna procedura optymalizacyjna wykorzystywana jest w bardziej życiowych zagadnieniach inżynierskich, o czym – w dalszej części artykułu.
Wykorzystanie optymalizacji w praktyce inżynierskiej
W praktycznych zastosowaniach wykorzystuje się oprogramowanie z wbudowanymi algorytmami do przeprowadzania procesu optymalizacji. Jednym z takich oprogramowań jest Isight dostarczany w pakiecie z Abaqusem przez firmę Dassault Systemes. W tym artykule postaram się opisać jak może wyglądać proces optymalizacji na przykładzie plastikowego klipsa, który można znaleźć w prawie każdym sportowym plecaku (Rys. 3). W poniższym przykładzie przedstawię uproszczony, dwuwymiarowy model, który znacząco pozwolił mi zredukować czas obliczeń. Jak łatwo się domyślić przy dziesiątkach symulacji każda sekunda obliczeń ma znaczenie.
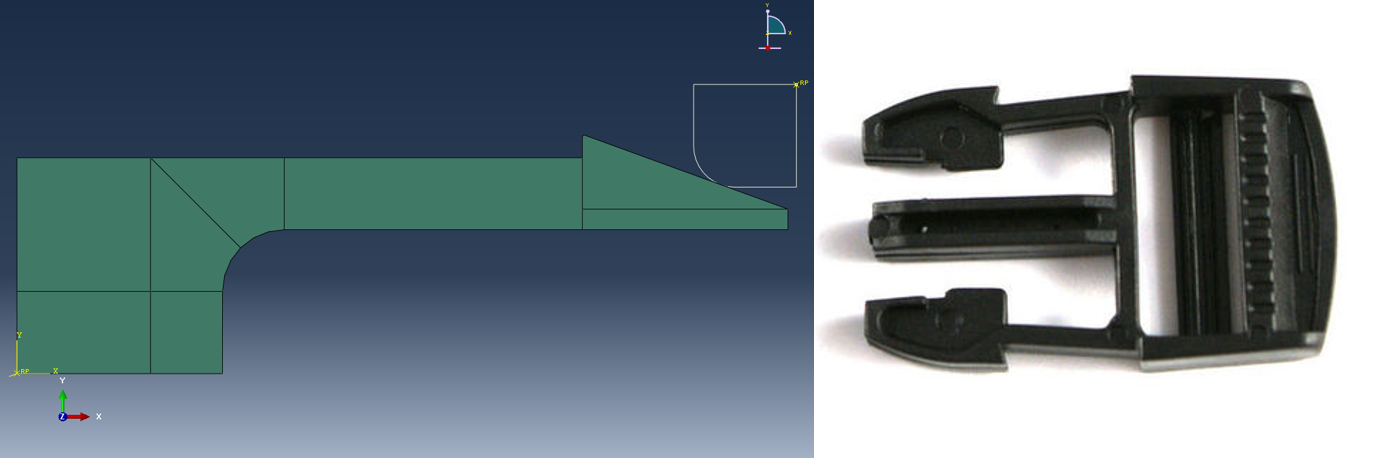
Rys. 3 Komputerowy (po lewej) i rzeczywisty (po prawej) model klipsa
Pierwszą decyzją, którą należy podjąć przed rozpoczęciem optymalizacji jest zdecydowanie, jaki jest jej cel. Optymalizacja parametryczna umożliwia nam sterowanie zachowaniem i właściwościami dowolnego obiektu pod warunkiem, że da się go zasymulować. Typowymi funkcjami celu jest minimalizacja wagi obiektu czy minimalizacja naprężeń. W naszym przykładzie zdecydowałem się na minimalizację naprężeń, co oznacza, że chcę zmniejszyć ryzyko zniszczenia klipsa podczas jego pracy.
Kolejnym krokiem jest określenie, które parametry klipsa zmniejszają bądź zwiększają jego wytrzymałość. Te parametry to tzw. zmienne optymalizacyjne i to one będą podane na wejściu do pętli optymalizacyjnej. Na pierwszy rzut oka można wymienić kilka z nich: a) wymiary klipsa, b) materiał z jakiego wykonany jest klips, c) temperatura w jakiej pracuje klips, d) dokładność wykonania.
Na tym etapie należy podjąć decyzję odnośnie tego, który czynnik jest decydujący. Czasem zdarza się tak, że zmuszeni jesteśmy wybrać ten czynnik, na który po prostu mamy wpływ. Projektując taki mechanizm mamy wpływ na to jakie ma wymiary i z czego jest wykonany. W tym przykładzie założyłem jednak, że to nie my, a klient decyduje o materiale, a my jako konstruktorzy mamy wpływ tylko na jego wymiary.
Kolejne pytanie, które musimy sobie zadać, to pytanie o to, które wymiary są istotne z perspektywy optymalizacji. Wybór zbyt dużej ilości zmiennych spowoduje, że proces optymalizacji będzie trwał bardzo długo. Co więcej, musimy także określić jakie minimalne i maksymalne wartości mogą przyjmować te wymiary. Po wstępnej inspekcji modelu postanowiłem, że wymiarami, które będą ulegać zmianie podczas optymalizacji będą wymiary przedstawione na rysunku 4 i w tabeli 1. Zakładam, że tak jak czytelnik artykułu, w tej chwili jeszcze niewiele wiem odnośnie tego, które wymiary mają największy wpływ na wytrzymałość.

Rys. 4 Szkic początkowy geometrii klipsa
| Wymiar | Wartość minimalna | Wartość maksymalna |
| α | 55° | 77° |
| T | 0,5 mm | 3,0 mm |
| L | 10,0 mm | 17,5 mm |
| R | 0,5 mm | 2,5 mm |
Tab. 1 Zestawienie wymiarów wykorzystanych w procesie optymalizacji
Mając tak zdefiniowaną tabelkę wymiarów można zacząć budowę pętli optymalizacyjnej. Pętla optymalizacyjna w Isight składa się z dwóch komponentów. Pierwszy odpowiedzialny jest za proces optymalizacji, drugi zaś za proces symulacji. Komponent optymalizacyjny umożliwia nam wybór odpowiedniego algorytmu optymalizacyjnego, co powoduje, że stajemy przed kolejnym dylematem. Mianowicie, który algorytm jest dla nas odpowiedni? Niestety na to pytanie nie ma jednoznacznej odpowiedzi, a wybór odpowiedniego algorytmu często jest rezultatem metody prób i błędów. Całe szczęście, że program jest na tyle pomocny, że przy każdym algorytmie zawarty jest opis zastosowania (Rys. 5). W oparciu o ten opis stwierdziłem, że algorytm NLPQLP będzie dobrym wyborem.
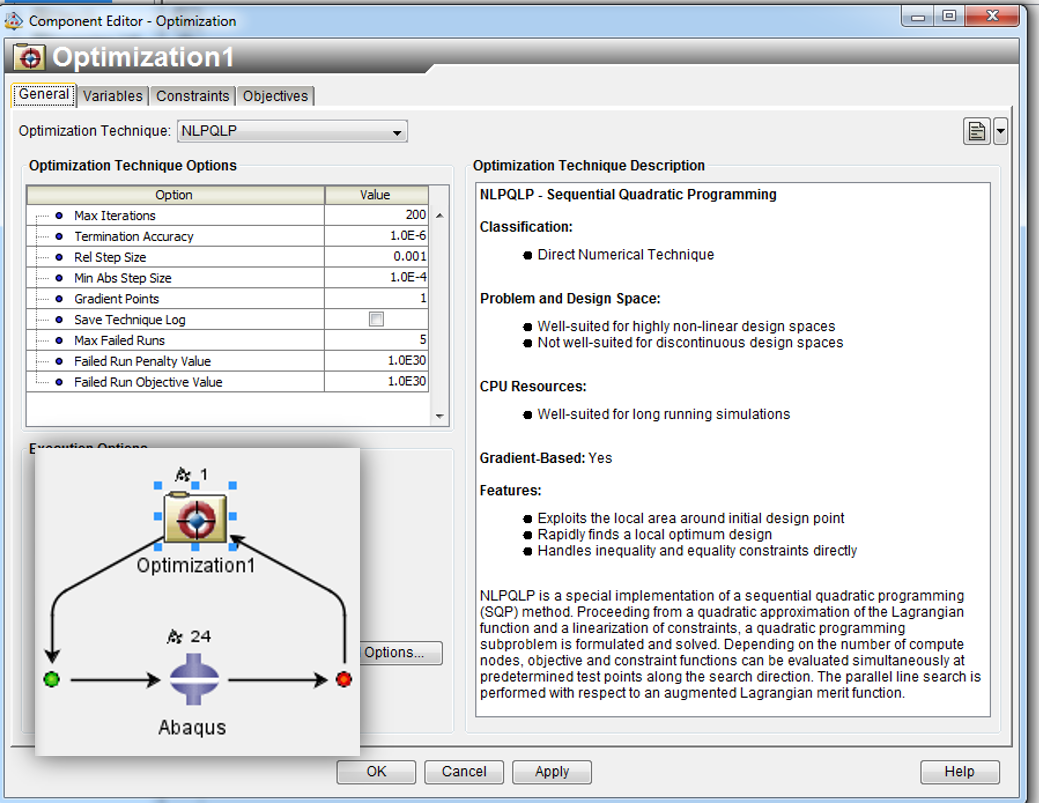
Rys. 5 Definicja komponentu optymalizacyjnego w Isight
Definicja komponentu symulacyjnego składa się importu modelu z Abaqusa oraz wyznaczenie wymiarów biorących udział w optymalizacji. Isight podczas optymalizacji sam modyfikuje wymiary oraz nakłada nową siatkę. W bardziej skomplikowanych zagadnieniach będzie trzeba mu nieco pomóc, ale generalnie połączenie na linii Isight-Abaqus działa bardzo dobrze.
Na tym etapie nie pozostaje nam nic innego jak uruchomienie pętli optymalizacyjnej. Wyniki z optymalizacji zostaną nam przedstawione w formie tabeli (Rys. 6), a kolorem zielonym podświetlony zostanie najbardziej optymalny zestaw wymiarów.
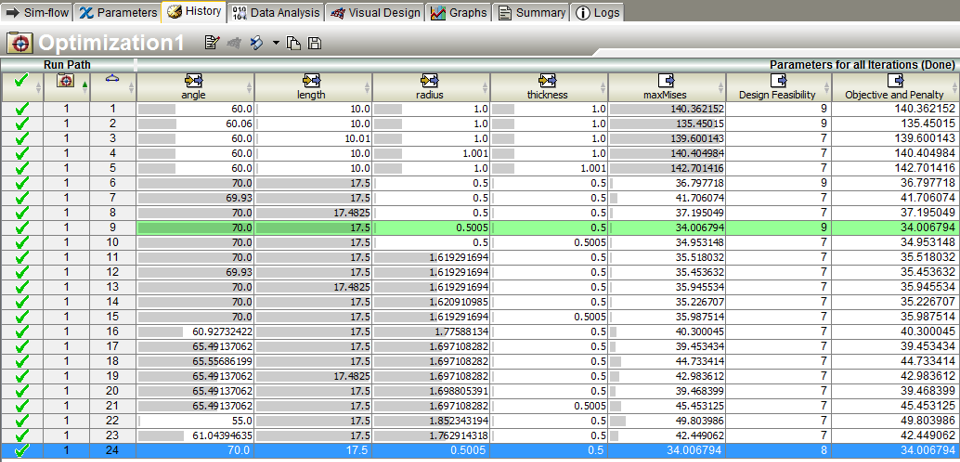
Rys. 6 Tabelaryczne zestawienie wyników z procesu optymalizacji
W ten prosty sposób program znalazł nowy zestaw wymiarów, dla którego maksymalna wartość naprężeń zmalała o prawie 100 MPa i wynosi teraz 34 MPa. Zakładając, że materiał ulega uplastycznieniu przy 70 MPa można powiedzieć, że modyfikacja, którą wdrożyliśmy z pewnością wydłużyła żywotność naszego klipsa.
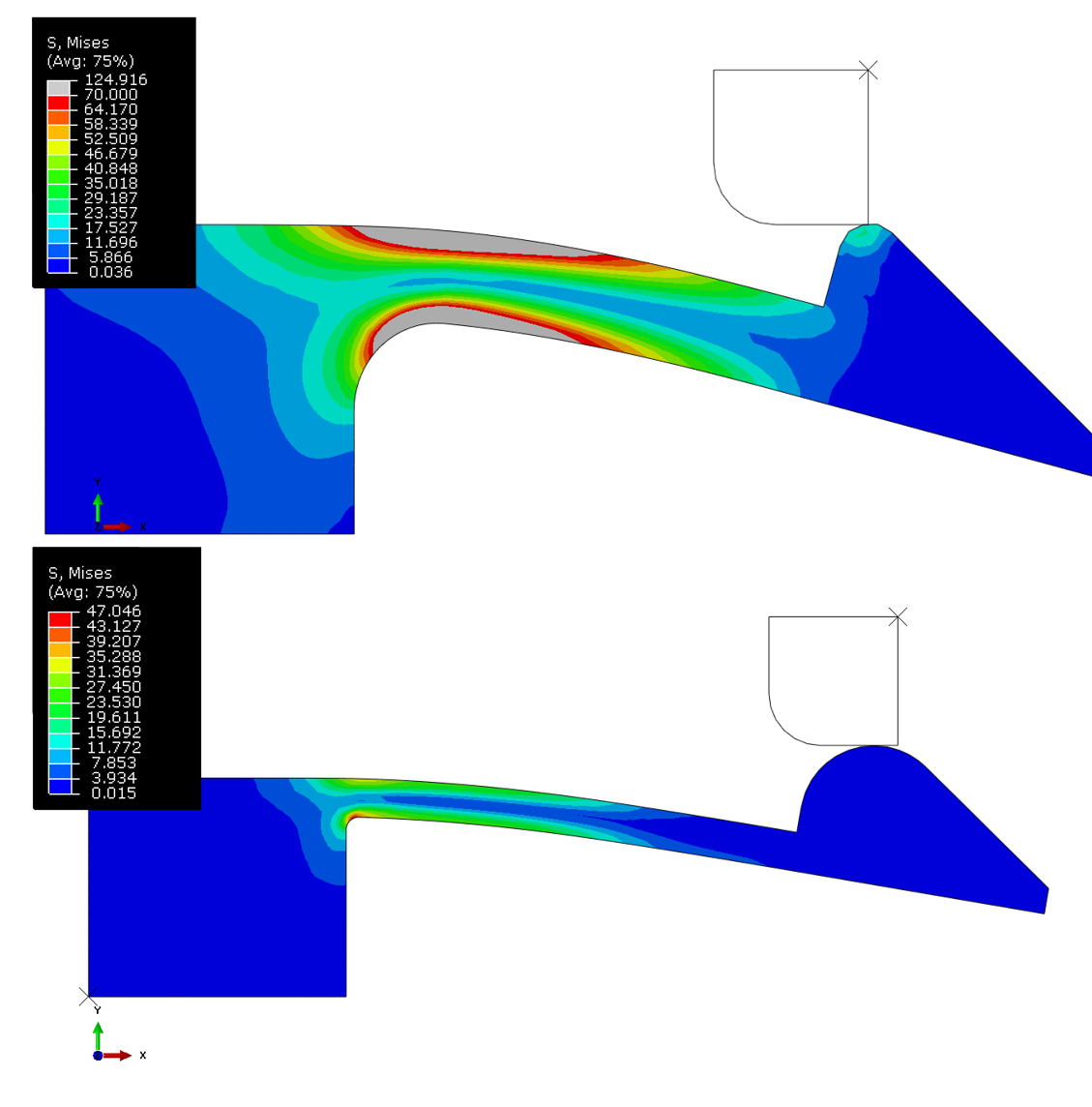
Rys. 7 Porównanie początkowej i zoptymalizowanej geometrii klipsa
Metoda planowania eksperymentu jako pośredni sposób optymalizacji
Wyobraźmy sobie sytuację, w której klient zadecydował, że minimalne wartości naprężeń są równie istotne co minimalna wartość siły potrzebnej na domknięcie mechanizmu klipsa. Proces optymalizacji ulega skomplikowaniu, ponieważ mamy do czynienia z dwiema funkcjami celu – jednocześnie zależy nam na zmniejszeniu wartości naprężeń oraz zmniejszeniu wartości siły. W takich przypadkach warto zastanowić się czy pętla optymalizacyjna jest najlepszym rozwiązaniem.
Z pośród wielu sposobów na znalezienie odpowiednich wymiarów klipsa w takiej sytuacji, postanowiłem wykorzystać coś co w literaturze angielskojęzycznej nazywa się Design of Experiments (DoE), a po polsku – metodą planowania eksperymentów. Chcąc wyjaśnić czym jest analiza DoE postaram się użyć pewnej analogii i odwołać się do wyobraźni czytelnika.
Optymalizacja przedstawiona w poprzednim przykładzie przypomina w sposobie swojego działania nawigację samochodową. Zazwyczaj dzięki niej dotrzemy do wyznaczonego celu, ale zdarzają się przypadki, że nawigacja zwyczajnie się myli i obiera niewłaściwy kierunek.
Chcąc zrozumieć ideę metody planowania eksperymentów można sobie wyobrazić, że naszym zadaniem jest przejście przez las w środku nocy, w którym ktoś rozstawił lampiony, aby nam pomóc. Łatwo sobie wyobrazić, że im bliżej lampionu tym więcej widzimy i mniejsze ryzyko, że zrobimy sobie krzywdę. Niestety, las jest ogromny, a ilość lampionów jest ograniczona. W oparciu o taką analogię, można powiedzieć, że metoda planowania eksperymentów polega na takim doborze położenia lampionów, aby nasza wiedza na temat położenia w lesie była jak najlepsza.
W przypadku mechanizmu klipsa specjalne algorytmy w programie pozwalają na uzyskanie jak największej ilości wartościowych i wiarygodnych informacji o badanym obiekcie na podstawie jak najmniejszej liczby doświadczeń.
Wiedząc jaka jest różnica pomiędzy optymalizacją a metodą planowania eksperymentów możemy wrócić do dalszej części optymalizacji klipsa. Dla przypomnienia, teraz naszym celem będzie jego udoskonalenie poprzez jednoczesną minimalizację wartości naprężeń i siły potrzebnej do jego zamknięcia. W tym celu wykorzystam opisaną wcześniej metodę DoE.
Na potrzeby tego przykładu wykorzystam wcześniej stworzony model oraz zmodyfikowaną pętlę optymalizacyjną. Chcąc określić siłę potrzebną do zamknięcia mechanizmu klipsa wykorzystana zostanie siła reakcji z części utwierdzonej. Wartość tę należy dodać do definicji komponentu Abaqus w programie Isight. Dodatkowo, poprzednio utworzony komponent procesu optymalizacji w pętli należy zmienić na komponent DoE. Komponent DoE odpowiedzialny będzie za proces przeprowadzania eksperymentu i chcąc go w pełni zdefiniować należy wybrać odpowiedni algorytm jego działania. Do tego badania postanowiłem wybrać algorytm o nazwie Optimal Latin Hypercube, który jest rekomendowany przez twórców oprogramowania do typowych zadań inżynierskich (Rys. 8).

Rys. 8 Definicja komponentu DOE w Isight
Tak jak poprzednio, tak i teraz wyniki z symulacji zestawione zostały w tabeli (Rys. 9). Warto wspomnieć, że sposobów na analizę wyników z programu Isight jest całe mnóstwo. Jednym z wykresów, często stosowanych w zagadnieniach inżynierskich, jest wykres Pareto. Informuje on użytkownika, które zmienne mają największy procentowy wpływ na naszą funkcję celu. Dla przykładu, niebieski kolor przy zmiennej thickness oznacza, że zwiększając jej wartość będziemy zwiększać wartość naprężeń w modelu. Wykres nie informuje nas „o ile” zwiększymy wartość naprężeń, ale pokazuje nam, że wśród wszystkich zmiennych to właśnie zmienna thickness ma największy wpływ na naprężenia (Rys. 9). Taka informacja jest cenna zarówno dla osoby zajmującej się projektowaniem klipsów, jak i ich wytwarzaniem.
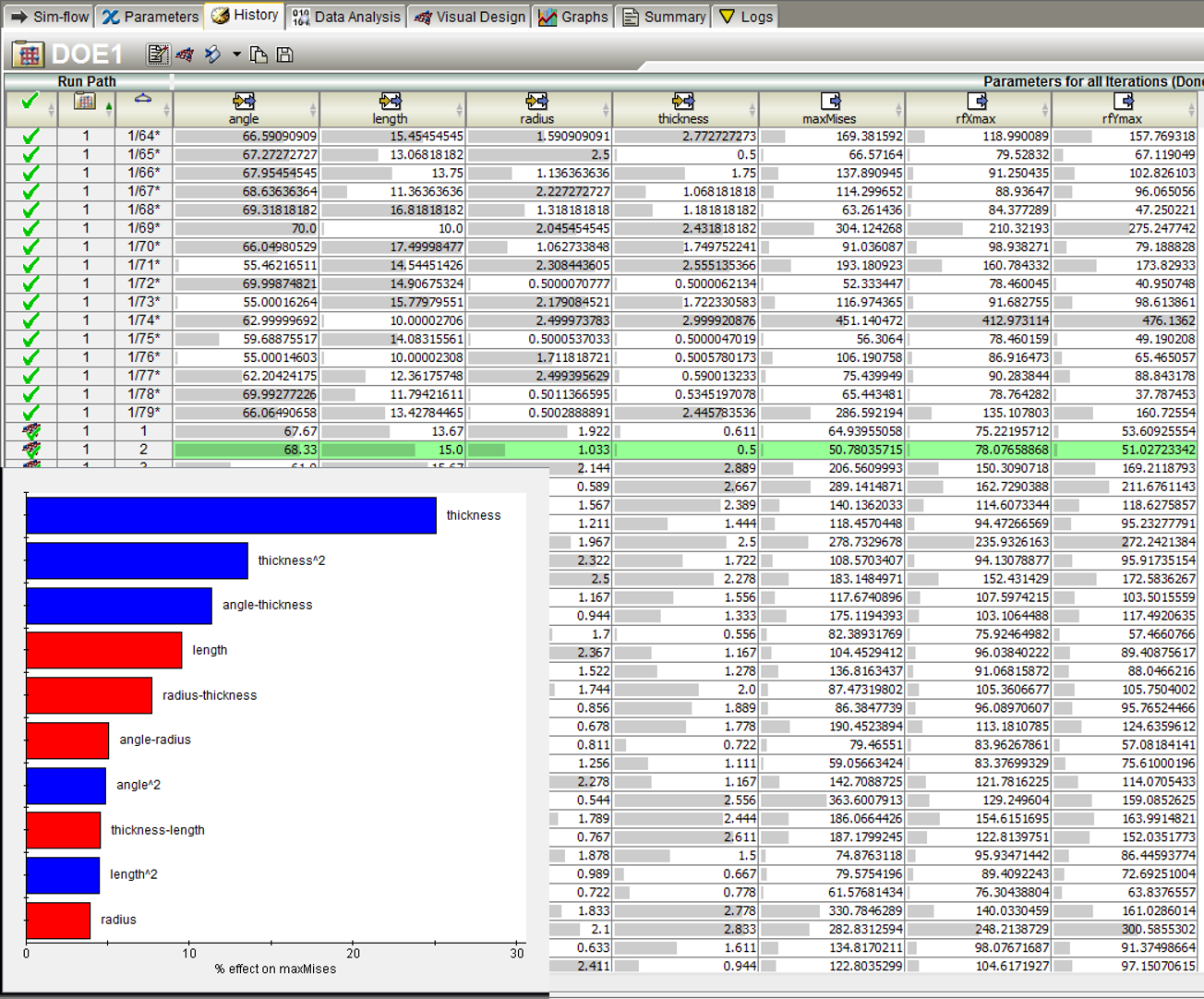
Rys. 9 Zestawienie tabelaryczne wyników oraz wykres Pareto
Podsumowanie
Mimo że przedstawiony przykład mechanizmu klipsa jest bardzo prosty to umożliwia zrozumienie jak wiele cennych informacji daje optymalizacja konstrukcji z wykorzystaniem symulacji komputerowych. Co więcej, takie narzędzia jak Isight nie służą tylko do optymalizacji – to środowiska zawierające mnóstwo narzędzi statystycznych, pozwalające opisać badane zjawisko jeszcze dokładniej.
Czytelnikom chcącym spróbować swoich sił z optymalizacją chciałbym zostawić również kilka wskazówek, które pozwolą łatwiej przygotować cały proces:
- Model, który będzie poddany optymalizacji powinien być stabilny i przewidywalny. Jeżeli podczas wstępnych testów wykryliśmy, że dla niektórych wartości zmiennych symulacja zakończona zostaje błędem to bardzo prawdopodobne, że te błędy wystąpią również w czasie trwania pętli optymalizacyjnej.
- Dobór odpowiednich zmiennych jest niesamowicie istotny dla końcowego rezultatu. Z tego powodu warto optymalizować te komponenty, których zasadę działania dobrze znamy.
- W przypadku doboru wymiarów komponentu należy pamiętać, by zwymiarować obiekt tak, aby zniwelować wzajemną zależność od siebie.
- Podczas ustalania wartości minimalnych i maksymalnych warto pamiętać o tym, żeby przedział wartości nie był zbyt duży, ponieważ dokładne odwzorowanie tego przedziału może być nieefektywne. Z drugiej strony warto pamiętać, że zbyt mały przedział wartości może nie ukazywać zmienności funkcji celu.
Sławomir Polański
Artykuł pochodzi z wydania styczeń/luty 1/2 (160/161) 2021