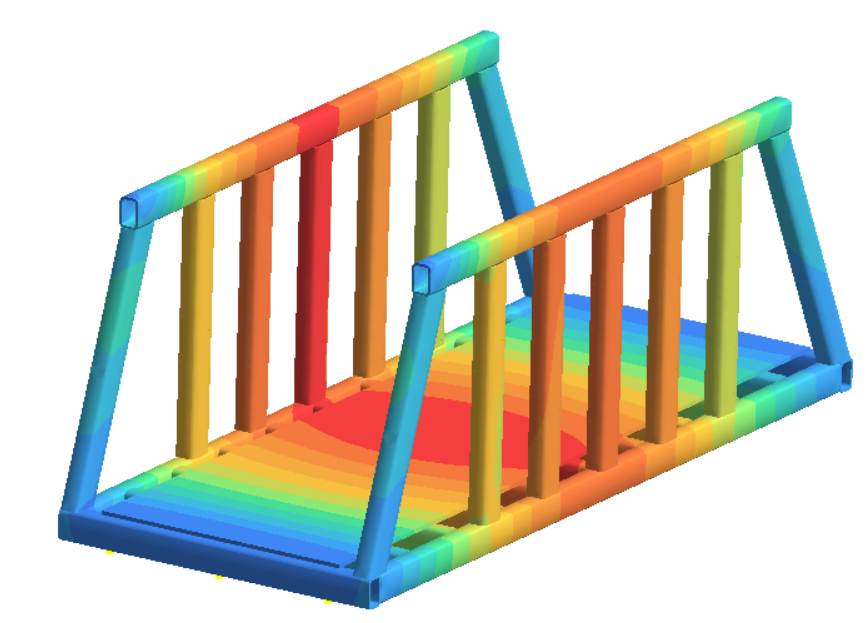
Symulacje numeryczne przy wykorzystaniu programów CAE pozwalają na szybką oraz tanią weryfikację i walidację produktu już na etapie fazy projektowania. Umożliwia to znaczne zredukowanie lub nawet wyeliminowanie kosztownych produktów koncepcyjnych. Ponadto dostępne są również narzędzia umożliwiające optymalizację rozwiązania na długo przed pierwszymi testami rzeczywistymi. Dzisiaj główną metodą wykorzystywaną przy tego typu zadaniach jest metoda elementów skończonych (MES, ang. FEM).
Maciej Majerczak
Metoda elementów skończonych ma duże grono zwolenników, jednak należy również pamiętać o jej niedoskonałościach i ograniczeniach. Jedną z takich wad jest potrzeba dyskretyzacji skomplikowanej geometrii na proste elementy składowe. Wynikowo otrzymujemy tu model składający się z dużej ilości elementów bardzo prostego kształtu. W zależności od wybranej metody modelowania rozróżnić możemy elementy przestrzenne, jakimi są przeważnie czworościany oraz prostopadłościany, lub elementy powłokowe, takie jak trójkąty i prostokąty. Należy zaznaczyć, że przygotowanie siatki elementów skończonych jest procesem trudnym, szczególnie gdy mamy do czynienia ze skomplikowaną geometrią, z dużą ilością cech takich jak promienie, krótkie krawędzie, małe powierzchnie, otwory itd.
Rozwiązać ten problem można na dwa sposoby: upraszczając geometrię – co jest zadaniem nietrywialnym, lub zdać się na zaawansowane algorytmy meshujące. Na rynku istnieje wiele rozwiązań pozwalających automatycznie przygotować siatkę o zadowalających parametrach. Jest to jednak proces stosunkowo czaso- i zasobochłonny. Dodatkowo musimy zmierzyć się z problemem wyboru dokładności lub szybkości rozwiązania. Gdy wybierzemy dokładność, przygotowany przez algorytm model może składać się z bardzo dużej ilości elementów, przez co wymagane będzie użycie znacznie większych zasobów komputerowych.
Odmiennym rozwiązaniem przedstawionego wyżej problemu jest metoda bezsiatkowa. Mowa tutaj o prawdziwej metodzie eliminującej potrzebę upraszczania geometrii i jej siatkowania, a nie takiej, która zgrabnie ukrywa siatkę elementów skończonych przed oczami użytkownika. Przedstawione rozwiązanie bazuje na teorii zawartej w “The Method of External Finite Element Approximations” opisanej przez Victora Apanovitcha.
Cały artykuł dostępny jest w wydaniu płatnym 7/8 (178/179) Lipiec/Sierpień 2022