Rozwiązywanie równań różniczkowych cząstkowych wymaga znajomości zaawansowanego aparatu matematycznego. Dla prostych przypadków jesteśmy w stanie uzyskać rozwiązanie analityczne, dla przypadków złożonych najczęściej jest to niemożliwe. Jedną z metod numerycznego rozwiązywania równań cząstkowych jest metoda objętości skończonych, która polega na podziale analizowanego obszaru na małe elementy kontrolne i przeprowadzenia po nich całkowania. Kształt elementu kontrolnego może być dowolny, co jest jedną z przyczyn dużej popularności tej metody, zwłaszcza do rozwiązywania równań mechaniki płynów.

Adam Piechna

W niniejszym artykule zastosujemy metody objętości skończonych do zamodelowania dwóch zagadnień: przewodzenia ciepła w pręcie i rozkładu ciśnień w szczelinie pomiędzy pierścieniem tłokowym a ścianą cylindra.
Wykorzystanie metody objętości skończonych przedstawimy na przykładzie równania dyfuzji. Ogólna postać równania jest następująca:



gdzie :
Φ – zmienna, której rozkładu szukamy
Γ – współczynnik dyfuzji; w ogólnym przypadku może być zależny od x
S – człony źródłowe
Ideą metody objętości skończonych jest podział analizowanego obszaru na skończenie małe objętości tzw. objętości kontrolne i przeprowadzenie po nich całkowania. Schematyczny podział obiektu jednowymiarowego przedstawiono na rysunku 1.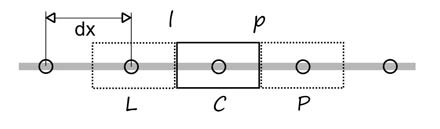



Rys. 1 Dyskretyzacja (podział) obiektu 1D na objętości kontrolne. Analizowana objętość kontrolna ma środek w punkcie C. Indeksami L i P oznaczono kolejno: lewą komórkę i prawą komórkę. Indeksami l i p oznaczono powierzchnie pomiędzy komórką centralną, a komórkami po lewej i prawej stronie.

Po dokonaniu podziału interesującego nas obszaru możemy wykonać całkowanie po wydzielonych objętościach:



Stosując twierdzenie Ostrogradskiego-Gaussa możemy zamienić całki objętościowe na całki powierzchniowe. W najprostszym przypadku 1D, stosując oznaczenia jak na rysunku 1 otrzymamy: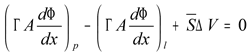



Przyjmując  Γ = const., A = const., dx = const. (W ogólnym przypadku  Γ , A, dx mogą być funkcją x) oraz zamieniając różniczkę na różnicę otrzymamy: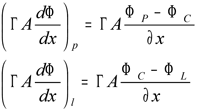



Podstawiając otrzymujemy: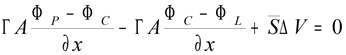



Porządkując otrzymujemy: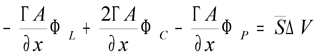



Jest to równanie algebraiczne liniowe opisujące zależności pomiędzy trzema elementami. Dzieląc analizowany obszar na przykład na pięć elementów musimy sformułować układ równań składający się z pięciu równań – po jednym dla każdego elementu kontrolnego. Równania dla elementu pierwszego i ostatniego będą różnić się od pozostałych. Elementy te są elementami brzegowymi i konieczne jest zdefiniowanie tzw. warunku brzegowego. Dwa typowe warunki to tzw. warunek Dirichlet’a (wartość zmiennej na brzegu) i Neumann’a (wartość pochodnej na brzegu). Rozpisując równania dla przykładu pięciu elementów otrzymamy układ równań :



W postaci macierzowej :



Równania w takiej postaci są bardzo proste do rozwiązania np. korzystając ze środowisk obliczeniowych GNU Octave (darmowe) lub Matlab.