Analiza rozkładu ciśnień w szczelinie pomiędzy pierścieniem tłokowym a ścianą cylindra
Takie same podejście możemy zastosować do analizy rozkładu ciśnień w wypełnionej olejem szczelinie pomiędzy pierścieniem tłokowym a ścianą cylindra.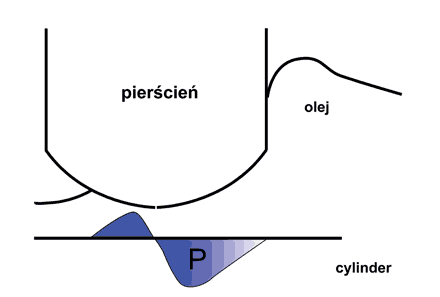
Rys. 4 Schemat analizowanego zagadnienia. Szukany rozkład ciśnienia w szczelinie pomiędzy pierścieniem tłokowym a ścianą cylindra.
Rozkład ciśnienia w szczelinie wypełnionej cieczą opisany jest równaniem Reynold'sa: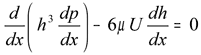
gdzie :
p – ciśnienie
h – lokalna wysokość szczeliny
U – prędkość pierścienia
μ – lepkość dynamiczna oleju
Przeprowadźmy analogiczny tok postępowania :
Tym razem współczynnik przy pochodnej jest również funkcją x:
Poniżej rozwiązanie problemu w środowisku GNU Octave. Konieczne było stworzenie dodatkowego skryptu-funkcji opisującej kształt pierścienia.
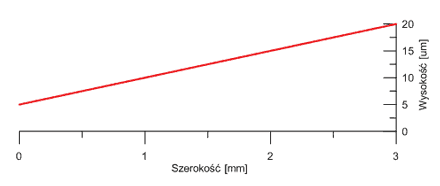



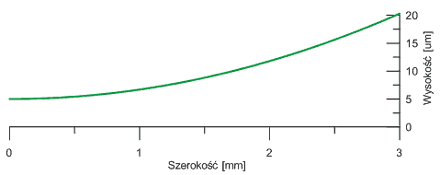



Poniżej otrzymane wyniki: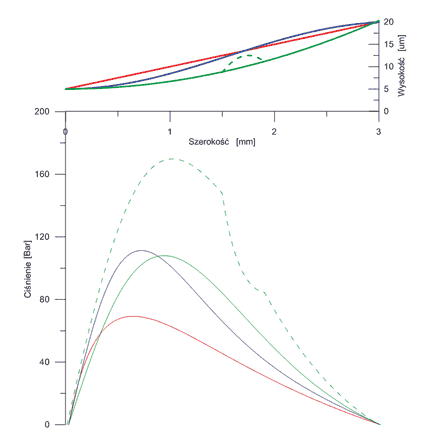
Rys. 5 Wyniki uzyskane w symulacji. Na górze – analizowane kształty pierścienia. Na dole – rozkład ciśnienia w szczelinie. Przerywaną linią oznaczony jest pierścień z defektem; obserwujemy znaczne zwiększenie panujących w szczelinie ciśnień.
Podsumowanie
W niniejszym artykule położyliśmy większy nacisk na pokazanie praktycznego wykorzystania metody niż na opis symulowanych zjawisk fizycznych.
Zachęcam do poeksperymentowania z zaproponowanymi modelami we własnym zakresie i do poświęcenia chwili na refleksję nad samą fizyką zjawisk. Przedstawiona metoda może zostać wykorzystana do rozwiązywania bardziej skomplikowanych dwu i trzywymiarowych zagadnień. Komplikuje się jednak wtedy proces dyskretyzacji analizowanego obszaru. Również liczba równań, którą trzeba rozwiązać wymaga zastosowania innego niż przedstawione podejścia.
Adam Piechna
artykuł pochodzi z wydania Czerwiec 6 (57) 2012
Czytaj także:
- start
- Poprzedni artykuł
- 1
- 2
- 3
- Następny artykuł
- koniec










