Kontynuując temat rozpoczęty w poprzednim miesiącu chciałbym tym razem skupić się nad metodami konstrukcji krzywych opisanych współrzędnymi biegunowymi.
Andrzej Wełyczko
Gdyby zadaniem konstruktora była konstrukcja krzywki płaskiej, której kształt jest opisany za pomocą spirali Archimedesa, to jedynym problemem może być geometryczna definicja tej krzywej w systemie CAD. Tu przypomnę jedynie, że ogólne równanie takiej krzywej to:
Rx = A ∙ φ; gdzie A jest stałą spirali lub inaczej jej skokiem.
Zalety takiej krzywej w zastosowaniach mechanicznych są oczywiste, bo Rx zmienia się liniowo wraz ze zmianą kąta φ. Inaczej mówiąc jeśli krzywka o takim kształcie obraca się ze stałą prędkością (argument φ rośnie liniowo), to popychacz styczny do krzywki porusza się ruchem jednostajnym (Rx zmienia się wprost proporcjonalnie do φ). W zastosowaniach praktycznych interesująca jest nie cała spirala Archimedesa, czyli cały zakres wartości φ z przedziału (0,∞), ale tylko jej niewielki fragment zaznaczony linią ciągłą na Rys.1:
W punkcie początkowym tej krzywej) Rx(β=0) = R,
Zmiana kąta β (od 0 do π) powoduje liniową zmianę wartości
Rx do Rmax(β=π) = R ∙ (1 + A ∙ β).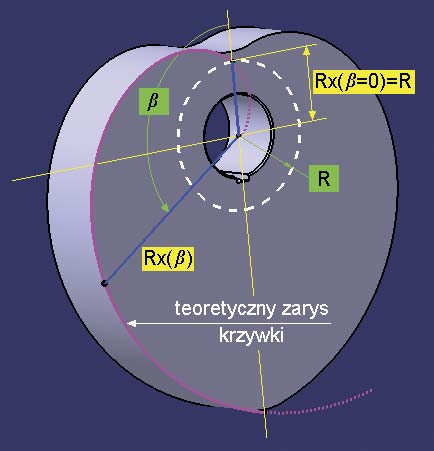
Rys. 1
Załóżmy, że dla krzywej BaseCircle (Rys.2) konstruktor zamierza wykreślić spiralę Archimedesa dla wartości A=1. Jeśli ta krzywa rzeczywiście jest okręgiem, to bez problemu można wyznaczyć płaszczyznę tej krzywej (CamCurvePlane), środek okręgu (BaseCircleCenter) oraz obliczyć jego promień (R=minimumCurvatureRadius(Input\BaseCircle).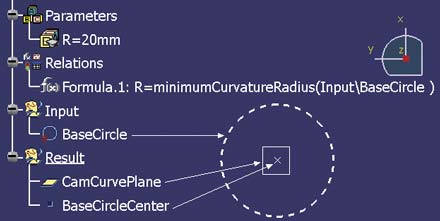
Rys. 2
Jeśli konstrukcja modelu geometrycznego spirali Archimedesa ma być wykonana zgodnie z opisaną w poprzednim odcinku procedurą (Parallel Curve + Law), to nie jest możliwe wskazanie krzywej zamkniętej BaseCircle (Rys.3).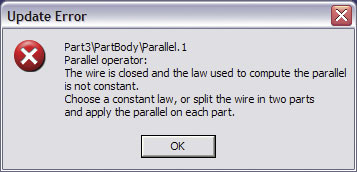 
Rys. 3
Dlaczego? Każda krzywa zamknięta ma swój punkt zamknięcia (Closing Point), który jest jednocześnie początkiem i końcem tej krzywej. Jaka wartość parametru Offset polecenia Parallel Curve ma być zastosowana do tego punktu: minimalna czy maksymalna?
Z tego powodu, ale także dlatego, że projektowana krzywka jest symetryczna można zdefiniować krzywą pomocniczą Split.1 (Rys.4), która będzie wskazana jako Curve w definicji krzywej typu Parallel Curve.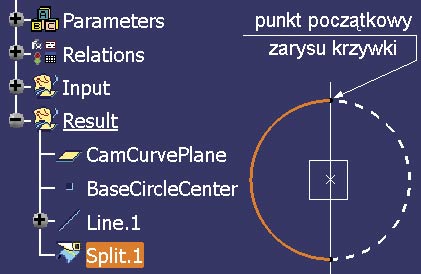
Rys. 4
Tu warto zatrzymać się na chwilę i zastanowić się nad tym, jak działa algorytm polecenia Parallel Curve. Położenie każdego punktu na dowolnej krzywej jest określone przez wewnętrzny parametr typu rzeczywistego (na przykład x), którego wartość zmienia się od 0 w punkcie początkowym do 1 w punkcie końcowym tej krzywej. Dla każdego punktu krzywej system znajduje kierunek prostopadły do krzywej w tym punkcie i na tej linii określa położenie punktu krzywej typu Parallel Curve. Celowo nie używam określenia krzywa równoległa, bo jeśli stosujemy prawo zmienności, to gdzie tu jest „równo”? Na przykład (Rys.5) dla x = 0,7 mamy:
Punkt Point.3 jest dowolnym punktem krzywej Split.1 (x = Point.3\Ratio = 0,7),
Linia Line.2 jest prostopadła do krzywej Split.1 w punkcie Point.3,
Punkt Point.4 leży na linii Line.2 w odległości
R ∙ (1 + x ∙ π) od punktu BaseCircleCenter (patrz równanie spirali Archimedesa dla A = 1 i β = x ∙ π) oraz w odległości R ∙ x ∙ π od punktu Point.3 (czyli krzywej Split.1).
Po tych wyjaśnieniach definicja prawa zmienności Law-Archimedes (Rys.6) jest chyba oczywista. Zamiast parametru x (typu Real) można zastosować parametr BETA (typu Angle) i wtedy prawo zmienności powinno być określone w następujący sposób:
Rx = R * BETA * PI/180deg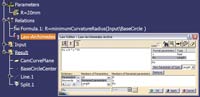
Rezultat zastosowania prawa Law-Archimedes, czyli krzywa Parallel.1 (Rys.7) jest poszukiwanym fragmentem spirali Archimedesa. Oczywiście w praktycznych zastosowaniach wartość parametru powinna być tak dobrana, aby uzyskać zakładany skok konstrukcyjny krzywki (tu dla A = 1 mamy Skok = R ∙ π).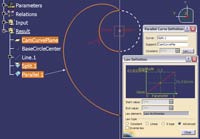
Taka metoda może być zastosowana w definicji różnego typu krzywych, ale dla spirali Archimedesa nie jest to metoda najprostsza. Wystarczy zauważyć, że ogólne równanie spirali Archimedesa jest funkcją liniową, a to oznacza, że w definicji krzywej typu Parallel Curve zamiast Law type = Advanced można wybrać Law type = Linear i zadać odpowiednie wartości Start value i End value (Rys.8).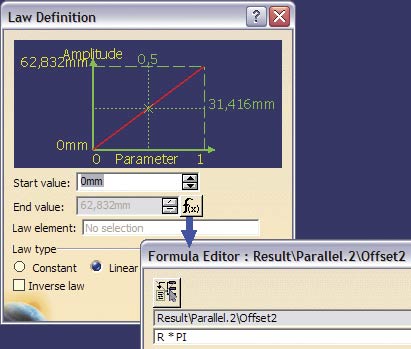
Rys. 8
Aby temat zakończyć trzeba jeszcze wykonać symetryczną kopię krzywej Parallel.1, zdefiniować łagodne przejścia dla wierzchołków takiego zarysu krzywki (Corner.1 na Rys.9), itd. Zadanie powinno być na tyle trywialne, że nie wymaga szczegółowego komentarza.
Czy taka metoda konstrukcji krzywej jest uniwersalna? Na przykład czy można ją zastosować w definicji ewolwenty koła (Rys.10)? Niestety metoda Parallel Curve + Law w definicji ewolwenty musi być nieco zmodyfikowana,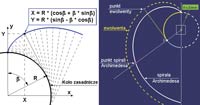
bo konieczne jest zastosowanie dwóch praw zmienności (dla parametrów X i Y). Szczegóły w następnym odcinku.
Andrzej Wełyczko
artykuł pochodzi z wydania 5 (20) maj 2009
