Manipulator posiada trzy stopnie swobody względem jego nieruchomej podstawy.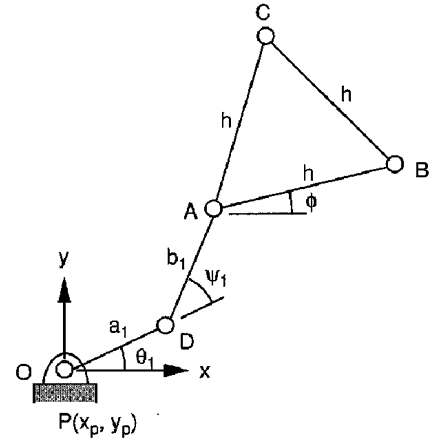
Rys. 3.1 Schemat struktury pojedynczego łańcucha kinematycznego manipulatora typu 3RRR
Geometria manipulatora typu 3RRR
W celu określenia geometrii manipulatora wprowadzono początek układu współrzędnych konstrukcji w punkcie P (rys. 2.1). Oś x przechodzi przez punkty PQ, a oś y jest do niej prostopadła i wyprowadzona z punku P. Założono, że zarówno ruchoma platforma ABC i podstawa PQR są trójkątami równobocznymi (AB = BC = AC = h i PQ = QR = RP = c). Na rysunku 3.1. pokazano zależności geometryczne i kątowe dla i kończyny (pojedynczego łańcucha) manipulatora. Współrzędne przegubów B oraz C możemy określić za pomocą współrzędnych przegubu A oraz kąta ϕ5: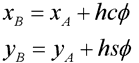
(3.1)
oraz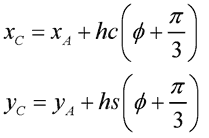
(3.2)
Na podstawie geometrii rysunku 3.1 przyjęto:![]()
(3.3)
możemy określić współrzędne punktu A10: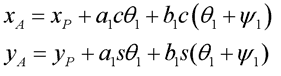
(3.4)
Punkt P znajduje się w początku układu współrzędnych, który przyjęło się określać układem odniesienia (względem tego układu rozpatruje się wszystkie obiekty łącznie z manipulatorem), przyjmując, że xP = yP = 0. Ponieważ kąt ψ1 jest kątem pasywnym to równanie (3.4) możemy przedstawić w postaci5: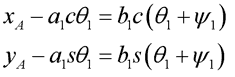
(3.5)
Potęgując i porównując równania (3.4) otrzymano:![]()
(3.6)
Podobnie, dwa dodatkowe równania mogą zostać wyprowadzone dla kończyn 2 i 3: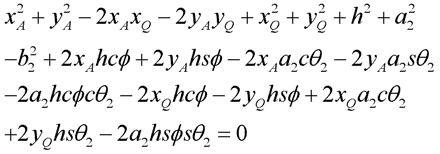
(3.7)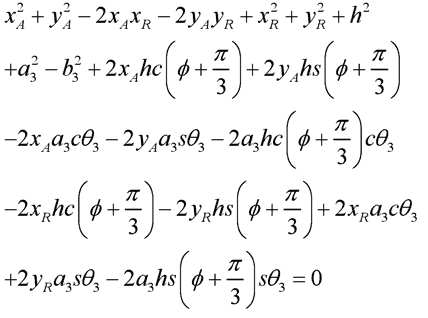
(3.8)
Projekt manipulatora o zamkniętym łańcuchu kinematycznym typu 3RRR z pneumatycznymi aktuatorami mięśniowymi
Strona 2 z 3
Specjalistyczny portal inżynierski dla osób zaangażowanych w tworzenie produktów – maszyn, urządzeń, mechanizmów, podzespołów, części, elementów itd. – od koncepcji do ostatecznego wykonania.






