Śp. ksiądz Jozef Tischner podał kiedyś w formie anegdoty podział na trzy rodzaje prawdy. Zastanawiałem się, jako stary inżynier, jak to jest w moim zawodzie konstruktora i doszedłem do wniosku, że w obszarze obliczeń inżynierskich jest bardzo podobnie. Też można wydzielić trzy grupy obliczeń.

Jerzy Mydlarz

Uważam, że obliczenia możemy uznać za prawdziwe, jeżeli niezależnie od tego kto je będzie realizował, dadzą wynik potwierdzony później z dużą dokładnością przez świat materialny. Do tej grupy należą, na przykład, obliczenia geometrii przekładni zębatej. Prawidłowy algorytm, niezależnie od tego czy jest obsługiwany przez nowicjusza czy też przez weterana, da poprawny, weryfikowalny wynik. To jest pierwszy rodzaj obliczeń.

Drugi rodzaj stanowią obliczenia empiryczne, zawierające dużą wiedzę ludzkości na temat fizyki zjawisk. Do tej grupy należą znormalizowane obliczenia dotyczące np. doboru parametrów przekładni przemysłowych. W tym obszarze doświadczenie osoby przeprowadzającej obliczenia ma już znaczący wpływ na wynik obliczeń. Zakres działania tej prawdy jest też ograniczony. Gdyby zastosować takie obliczenia do przekładni czołgowej, to w rezultacie przekładnia miałaby wielkość jednej trzeciej czołgu, a tak nie jest. Te metody i wzory zupełnie nie nadają się do przekładni pojazdów wyczynowych i lotnictwa. W tej samej grupie prawdy znajdują się podstawowe obliczenia wytrzymałościowe. Pokazują one pewne logiczne zależności pomiędzy naprężeniem materiału a działającą siłą i wielkością przekroju. Natomiast, jak to się ma do rzeczywistości trudno powiedzieć. Z pewnością wyznaczone przekroje są dla większości przypadków wystarczające w aspekcie bezpieczeństwa, a dzieje się to kosztem wielkości i ciężaru.
Jako młody konstruktor zajmowałem się przez pewien czas projektowaniem zawiesi. Zakład, w którym pracowałem posiadał własną kuźnię, spawalnię, hartownię i laboratorium. W tamtych czasach niewiele rzeczy można było kupić i sami wytwarzaliśmy elementy zawiesi. Jednym z nich było ogniwo zbieżne, przedstawione na rysunku 1.
Zaprojektowałem właśnie zawiesie zgodne z ówczesnymi normami. Zostało ono skierowane do wykonania. Ktoś popełnił błąd i okazało się po zmontowaniu zawiesia, że zostało nam jedno nowe, niepotrzebne ogniwo zbieżne. Mój dobry kolega był kierownikiem laboratorium wyposażonego w zrywarkę i namówiłem go, żeby sprawdzić jakie obciążenie zrywające wytrzyma ogniwo przewidziane wg PN na 50 kN. Wykonałem odpowiednie mocowania i przeprowadziliśmy próbę niszczącą. Trudno w to uwierzyć, ale ogniwo zerwało się pod obciążeniem ponad 1200 kN!

Trzeci rodzaj prawdziwości obliczeń stanowią czasem niektóre symulacje. Tutaj prawie wszystko zależy od kwalifikacji i doświadczenia osoby przeprowadzającej symulację. W czasie prowadzenia badań do mojej rozprawy doktorskiej, mój promotor, profesor dr hab. inż. Andrzej Baier, ekspert w zakresie badań symulacyjnych, wprowadzał mnie w zagadnienia symulacji ruchu pojazdu w module Motion Simulation programu NX. Podczas wprowadzania różnych parametrów do programu, bardzo często program informował, że wartość wstawiona do okienka przez sam program jest tylko wartością wstępną, którą można i należy zmienić, jeśli się posiada dane badawcze lub doświadczenie. Zatem wynik symulacji, co jest oczywiste, jest tylko pochodną tego co wstawimy na wstępie. Ja byłem w tej komfortowej sytuacji, że posiadałem redukcyjny model fizyczny i obserwując jego zachowanie w czasie prób ruchowych mogłem wpływać na zachowanie się pojazdu w świecie wirtualnym. Jednak, gdybym takiego modelu fizycznego nie posiadał, to uzyskane wyniki symulacji nie byłyby weryfikowane w żaden sposób. Istnieją też, na szczęście, symulacje bliskie pierwszemu rodzajowi prawdy. Znam ośrodki zajmujące się symulowaniem tylko jednego zjawiska, robiące to przez wiele lat. Ogrom zebranych doświadczeń sprawia, że w ich badaniach, wynik symulacji jest bardzo wiernym odzwierciedleniem świata realnego. Komercyjni klienci o tym wiedzą i ustawiają się w kolejce po wyniki takich obliczeń.
Proste obliczenia inżynierskie, które moim zdaniem należą do pierwszego rodzaju prawdy, chciałbym przedstawić poniżej. No, może są czymś pomiędzy pierwszym a drugim rodzajem prawdy.
Przez wiele lat zajmowałem się przekładniami zębatymi. W dawnych czasach obliczenia z nimi związane były żmudne i nudne, a wynik niepewny. Często kilka osób obliczało ten sam przypadek, aby zwiększyć pewność co do uzyskanego wyniku. Zanim pojawiły się komputery i nieoceniony arkusz kalkulacyjny, najczęściej stosowane obliczenia geometryczne realizowałem za pomocą kalkulatora programowalnego firmy CASIO, w języku zbliżonym do języka BASIC. Nowsze i lepsze wersje kalkulatorów nadal są w użytku i metodyka programowania jest taka sama, choć pewne wyższe modele pozwalają nawet na użycie języka C++. Obecnie, dzięki możliwości połączenia kalkulatora z komputerem przez port USB, jest nieco wygodniej. Metoda jest jednak dość złożona i wymaga trochę cierpliwości. Nie jest to niestety tak, że wchodzimy do kalkulatora przez komputer i piszemy program. Metodyka ta, jest w zasadzie materiałem na osobny artykuł.
Pierwszym programem, który bardzo ułatwił mi życie zawodowe był program do wyznaczania rzeczywistej odległości osi w przekładniach zębatych walcowych o zębach śrubowych korygowanych, z korekcją P tzn. dowolną na obu kołach zębatych. Technicznie chodziło o to, aby przy remoncie przekładni zębatej dobrać taką geometrię uzębienia, by nowe koła dały się zamontować do istniejącego korpusu z właściwym luzem. Częstokroć nieznane mi przekładnie przychodzące do remontu, miały tak zużyte lub całkowicie zniszczone koła zębate, że z trudem udawało się ustalić liczbę zębów. W oparciu o znane algorytmy ułożyłem program, który umożliwiał wielokrotne dobieranie wielkości modułu, współczynników korekcji kół i kąta pochylenia linii zęba tak, aby uzyskać odległość osi zmierzoną na korpusie przekładni. Program przedstawiam poniżej.

Aż trudno uwierzyć, że taki malutki programik może tak bardzo ułatwić życie konstruktora. Główną jego część stanowią kolejne przybliżenia mające na celu ustalenie wielkości argumentu tj. tocznego kąta przyporu α, przy którym funkcja inwolutowa przyjmuje określoną wartość. Ustalono doświadczalnie, że dokładność 0,001 stopnia w ostatniej pętli jest wystarczająca. Jest to klasyczna metoda iteracyjna. Funkcja inwolutowa w ogólnej postaci jest zapisana wzorem:

Inv α = tgα – α*π /180

W obliczeniach przekładni wylicza się wartość funkcji, a następnie trzeba odnaleźć wielkość argumentu, którym jest kąt α. W dawnych czasach do tego celu stosowało się tablice funkcji inwolutowej i z nich odczytywało poszukiwaną wielkość. Wartości odległości osi wyznaczone za pomocą przedstawionego programu są zgodne z wynikami uzyskiwanymi w programie Autodesk Inventor.
Drugim, w aspekcie częstotliwości stosowania, jest program do pomiaru koła zębatego przez n zębów. Jest to fundamentalna wielkość mająca wpływ na luz międzyzębny (obwodowy) przekładni. Jej znajomość jest potrzebna przy projektowaniu przekładni jak również przy frezowaniu i szlifowaniu uzębienia.

Również i ten bardzo użyteczny program nie poraża swoją wielkością i komplikacją.
Dygresja o luzie obwodowym: W przypadku rekonstrukcji zwykłych przekładni przemysłowych, można ten luz dobrać posługując się ogólnymi wytycznymi z Poradnika Mechanika lub dokładniej wg PN-79/M-88522.01. Utarło się, również w normach, że ujemną odchyłkę dla obu kół zębatych wyznacza się albo wg zaleceń dla danej klasy dokładności lub tradycyjnie dzieląc po połowie wartość założonego luzu. Zakładając luz w pewnych granicach, mamy wartości odchyłek. Takie podejście jest zasadne przy niewielkich przełożeniach, gdy obydwa współpracujące koła zębate mają zbliżone średnice. Przy znaczącej różnicy średnic kół, warto przenieść całkowitą ujemną odchyłkę wielkości luzu obwodowego na duże koło. Ma ono więcej zębów i biorąc pod uwagę ubytek materiału wskutek zużycia, jest to rozwiązanie bardziej racjonalne.
Kolejny program jest użyteczny przy pomiarze kół zębatych o uzębieniu wewnętrznym. Koła takie spotykamy najczęściej w przekładniach planetarnych. Program może być stosowany tylko do kół o zębach prostych korygowanych. Wylicza on w pierwszej kolejności teoretyczną średnicę wałeczków pomiarowych. Następnie pozwala dobrać wałeczek rzeczywisty tj. o wymiarze będącym najbliższym i łatwo osiągalnym. Przykładowo, gdy program wyliczy wartość średnicy równą 3,887 mm, to możemy dobrać wałeczek ϕ3,5 lub ϕ3,75 albo ϕ4. Oto zapis programu:

Program po wprowadzeniu danych zajmuje się wyznaczeniem wartości argumentu α funkcji inwolutowej, podobnie jak to było w programie do wyznaczania odległości osi. Następnie prowadzi rozróżnienie czy mamy do czynienia z parzystą czy nieparzystą liczbą zębów. Oto wiersze rozróżnienia:

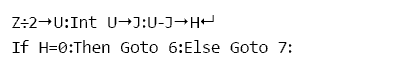
Funkcja Int (Integer) wyodrębnia część całkowitą z wyniku dzielenie liczby zębów Z i zapisuje ją w pamięci J. Następnie od wyniku dzielenia U odejmuje zawartość pamięci J. Jeżeli w wynikiem jest zero, to liczba zębów jest parzysta, i program kieruje dalsze obliczenia do etykiety 6. Jeżeli nie, to liczba zębów jest nieparzysta i obliczenia są kontynuowane od etykiety 7.
To rozróżnienie jest istotne, ponieważ wzory do wyznaczania wielkości pomiaru między wałeczkami różnią się dla obu rodzajów kół zębatych. W zasadzie można by zatrzymać program i rozróżnienie wprowadzić ręcznie, ale jest bardziej elegancko, jeśli program sam to robi. Po dokonaniu rozróżnienia następuje podstawienie wyznaczonej wcześniej wartości α do odpowiedniego wzoru i wyświetlenie wyniku.
Ostatecznie mamy jeszcze możliwość zmiany średnicy wałeczka pomiarowego lub powrót do początku obliczeń. Pewne nieuporządkowanie numerów etykiet wynika z rozwijania (przez lata) programu i jest zjawiskiem dość powszechnie spotykanym. Zgodnie z pragmatyczną zasadą: „ Jak działa, to nie ruszać!”
Bardzo podobnym programem jest program do pomiaru uzębień zewnętrznych przez wałeczki. Jest on przydatny do pomiarów uzębień sprzęgieł zębatych o zarysach ewolwentowych. Kąt zarysu odniesienia (zwany w programie kątem przyporu) wynoszący w sprzęgłach zębatych najczęściej 30o i współczynnik wysokości zęba 0,5 powodują, że mikrometr talerzykowy nie zawsze nadaje się do pomiaru przez n zębów. Sam program jest modyfikacją poprzedniego.

Na koniec muszę powiedzieć, że nie biorę odpowiedzialności za wszelkie skutki wynikłe ze stosowania przedstawionych tu programów. Wynika to z tego, że bardzo łatwo je popsuć, przez nieuważnie wprowadzanie, pomijając lub powtarzając jakiś symbol lub literę. Często z takimi defektami program dalej działa i liczy bzdury, czyli trzeci rodzaj prawdy.
Przedstawione programy można ułożyć w inny sposób. Moja maniera postępowania nie jest prawdopodobnie optymalna. Wynika ona z wielu lat zabawy z różnymi kalkulatorami programowalnymi. Jest to zapewne duże pole do popisu dla następców.
Nie lubię książek, w których uczeni mężowie prezentują różne wzory, ale stronią od przykładów obliczeniowych. Powstaje we mnie wówczas podejrzenie, że sami autorzy nie wierzą w moc swoich wywodów. Czasem pojawiają się przykłady, ale tyczą się one nieistniejących przekładni i zawierają błędy, których nigdy nie skorygowało życie. Zatem przejdźmy do realnego przykładu.