Przekładnie zębate są jednymi z najważniejszych elementów maszyn. Pozwalają na przekazywanie mocy oraz zmianę momentu i prędkości obrotowej. Umożliwiają sterowanie kinematyką danego obiektu w sposób prosty i przewidywalny. Z uwagi na ich szerokie zastosowanie, praktycznie we wszystkich gałęziach przemysłu, a w szczególności w przemyśle maszynowym, bardzo ważne jest nadzorowanie pracy tych – często bardzo skomplikowanych – układów.
Maciej Majerczak
Wyróżnić można trzy rodzaje serwisowania przekładni zębatych:
- Run-to-Break – tradycyjna metoda polegająca na pracy przekładni do czasu awarii,
- Prevent Maintenance – metoda polegająca na prewencyjnych serwisach, co określony czas,
- Condition-Based Maintenance – metoda polegająca na serwisowaniu przekładni w momencie kiedy wymaga tego urządzenie. Metoda ta bazuje na oczujnikowaniu przekładni i ciągłej analizie sygnałów uzyskiwanych podczas pracy.
Zdecydowanie najciekawszą, a zarazem najbardziej zaawansowaną metodą analizy jest sposób trzeci. Rozwijane są coraz to nowsze metody i algorytmy analizy sygnałów, jednak aby przetestować pewne założenia, a zarazem zminimalizować koszty testów, jak również wyeliminować niebezpieczeństwo zniszczenia często bardzo drogich przekładni zębatych, stosuje się modelowanie komputerowe.
Metody diagnostyki przekładni
Wyróżnić można kilka metod diagnostycznych, m.in. – pomiar temperatury podzespołów, oględziny elementów przekładni, jak również analiza oleju (jakość oleju oraz ilość znajdujących się w nim opiłków). Jednak najczęściej stosowanym rozwiązaniem jest metoda polegająca na analizie sygnałów drganiowych.
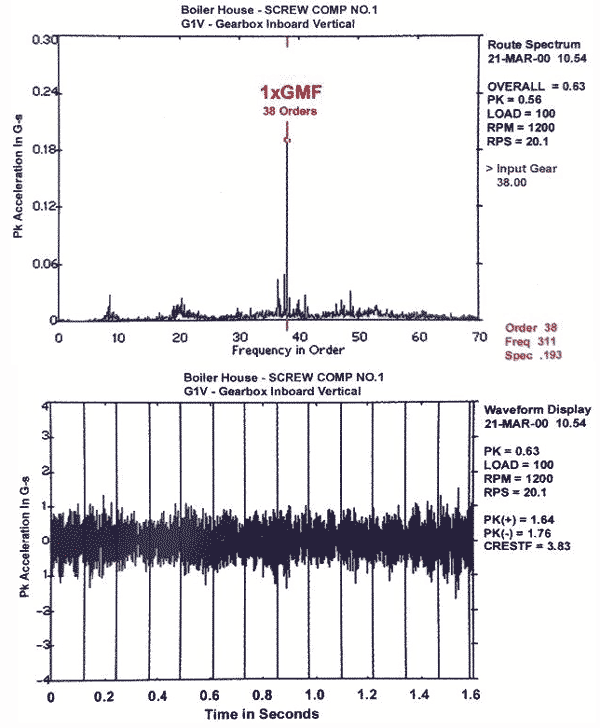
Rys. 1 Przykładowy sygnał przekładni bez uszkodzeń z mocnym komponentem GMF
Wibroakustyka jest bardzo często stosowaną metodą podczas wykrywania usterek w przekładniach zębatych. Analizę przeprowadza się badając przebieg czasowy prędkości lub przyśpieszenia drgań. Następnie sygnały te poddaje się dalszej obróbce, takiej jak FFT (Fast Fourier Transform – szybka transformata Fouriera). Tym sposobem sygnał wytwarzany przez maszynę podlega dekompozycji, czyli dzieli się go na poszczególne elementy składowe. Stąd też w oparciu o budowę maszyny oraz jej podstawowe parametry ruchowe, możliwe jest przypisanie poszczególnych elementów układu do składowych widma drgań. Tak przygotowany sygnał analizuje się za pomocą różnego rodzaju badań diagnostycznych. Bardzo często szczególną uwagę zwraca się na wartość skuteczną (RMS) prędkości drgań. Na podstawie tego parametru można ocenić energię niszczącą. Oprócz tego, diagnostyka pozwala na wykrycie przyczyn wysokich wartości wibracji. Jednym z najważniejszych założeń diagnostyki drganiowej jest określenie czasu, w jakim przekładnia może być eksploatowana. Właściwie przeprowadzona diagnostyka powinna dostarczyć dane niezbędne do określenia i wykonania działań korygujących, tak aby szybko i tanio wyeliminować zagrożenie.
Modelowanie przekładni zębatych
Aby zamodelować przekładnię zębatą wraz z uszkodzeniami, wykorzystamy połączenie dwóch metod analizy komputerowej – analizę typu MultiBody (metoda brył sztywnych) oraz metodę elementów skończonych, w celu odwzorowania kół zębatych jako ciał odkształcalnych.
Jako przykład posłużą nam model oraz analiza prostego układu równoległego, złożonego z dwóch kół zębatych o zębach prostych (Rys. 2).

Rys. 2 Model przekładni zębatej wraz z podstawowymi parametrami
Możliwe jest również analogiczne przygotowanie znacznie bardziej skomplikowanych układów, zawierających wielostopniowe przekładnie planetarne, wraz z odkształcalnymi wałami, oraz modelami komputerowymi łożysk.
Zdecydowaliśmy się na wprowadzenie uszkodzenia w postaci nadpęknięcia zęba u jego podstawy. Przygotowano trzy modele przedstawiające różne jego stopnie: małe pęknięcie, większe uszkodzenie oraz poważny ubytek (Rys. 3).
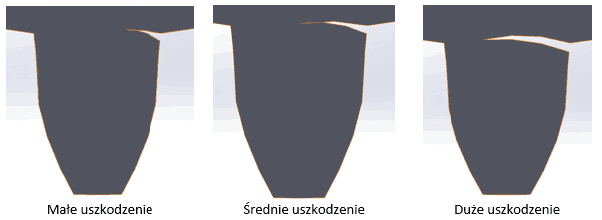
Rys. 3 Różne rozmiary wprowadzonych uszkodzeń
Analizowany model został przygotowany w środowisku MSC Nastran oraz ADAMS.
Pierwszym krokiem było przygotowanie modelu CAD. W tym celu wykorzystany został moduł zawarty w programie ADAMS, gdzie po wprowadzeniu kilku podstawowych parametrów, generowana jest dokładna geometria kół zębatych. Następnie model ten eksportujemy jako geometrię CAD, tak aby możliwe było przygotowanie siatki elementów skończonych, co jest kolejnym krokiem procesu.
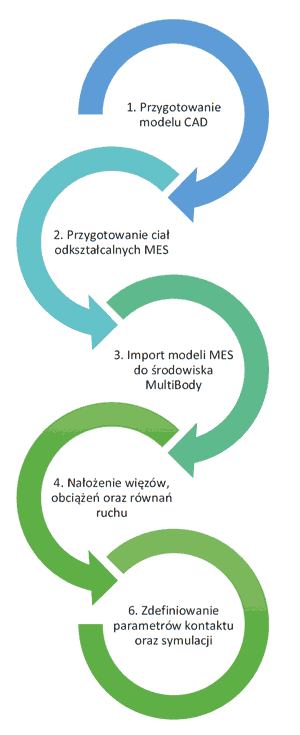
Rys. 4 Uproszczony schemat przygotowania modelu do analizy przekładni
Analizowany model cechuje się bardzo prostą geometrią, przez co zalecane jest przygotowanie siatki z wykorzystaniem elementów sześciennych typu HEXA. Zabieg ten pozwoli znacząco zredukować ilość elementów oraz pozwoli na wykorzystanie elementów pierwszego rzędu, przez co czas obliczeń oraz potrzebne zasoby obliczeniowe zostaną znacznie zredukowane. Alternatywą jest wykorzystanie elementów czworościennych typu TETRA, jednak należy tutaj pamiętać, że w tym przypadku wygenerowanych zostanie większa ilość elementów, jak również niezbędne jest zastosowanie elementów drugiego rzędu, w celu uzyskania poprawnych wyników. Natomiast ogromną zaletą tej metody jest możliwość przygotowania siatki przy pomocy auto-meshera (Rys. 5).

Rys. 5 Siatka elementów skończonych typu TETRA
Po przygotowaniu modeli MES, należy przygotować modele ciał odkształcalnych, które będą mogły zostać zaimportowane do programu przeznaczonego do analizy typu MultiBody. Dla solvera Nastran są to pliki MNF (modal neural file), które zawierają reprezentacje ciała odkształcalnego (flexible body), bazującą na modach rezonansowych. Aby otrzymać tego typu pliki, należy przygotować prostą analizę modalną dla każdego z kół zębatych oddzielnie, z uwzględnionymi wszystkimi warunkami brzegowymi. Na koniec należy dodatkowo zażądać od solvera wygenerowania pliku MNF. Krok ten należy powtórzyć dla modeli z różnymi uszkodzeniami.
Ostatnim etapem jest wczytanie otrzymanych plików MNF do pakietu ADAMS. Na zakończenie należy przygotować pełną analizę MultiBody, czyli nałożyć więzy, ograniczenia oraz kontakt pomiędzy ciałami. Ważne jest również wybranie miejsc, z których będziemy odczytywać wartości przyspieszeń. Po przeprowadzeniu obliczeń można przejść do analizy uzyskanych wyników.
Analiza uzyskanych wyników
Jak wspomniano wcześniej, przeanalizowana została prosta przekładnia równoległa, o piętnastu oraz osiemnastu zębach. Założono prędkość obrotową koła napędzającego równą 3600 RPM (obrotów na minutę), co odpowiada częstotliwości 60 Hz. Przeliczając kinematykę przekładni łatwo można wyliczyć, że koło osiemanstozębowe będzie się obracać z prędkością obrotową 3000 RPM czyli 50 Hz. Tabela 1 przedstawia podstawowe częstotliwości dla badanej przekładni zębatej.
Tab.1
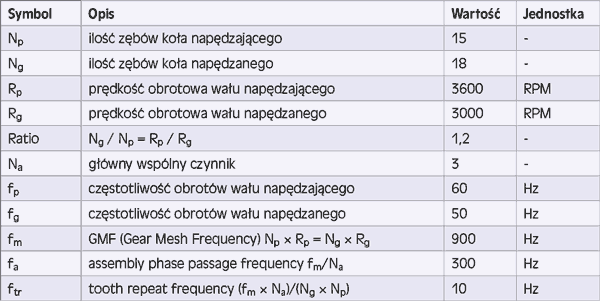
Zgodnie z oczekiwaniami, wprowadzone uszkodzenia wpłynęły na uzyskany sygnał drganiowy. Analizując częstotliwości GMF można zauważyć, że dla modelu z największym uszkodzeniem zęba, wartości GMF są od 6 do 13% wyższe niż dla modeli bez uszkodzeń. Jednak znacznie ciekawsze spostrzeżenia można zaobserwować analizując częstotliwości niższe od GMF. Zauważono mocne piki, generowane przez model z najbardziej uszkodzonym zębem. Impulsy te oddalone są od siebie o 50 Hz czyli o częstotliwość równą jednemu pełnemu obrotowi wału, na którym osadzono koło z uszkodzonym zębem. Należy ponadto pamiętać, że dla niższych częstotliwości bardziej odpowiednia jest analiza sygnału prędkości liniowej, dlatego zbadano widmo właśnie takiego sygnału. Na rysunku 6 można zaobserwować, że prążki układają się w podobną zależność jak obserwowano przy analizie częstotliwości GMF.
Rys. 6 Wartości przyspieszeń dla częstotliwości niższych od pierwszego GMF
Im bardziej uszkodzone koło zębate, tym większe wartości prędkości uzyskujemy w poszczególnych częstotliwościach. Warto również zaznaczyć, że dla koła bez uszkodzenia, praktycznie nie obserwuje się występowania takich częstotliwości na widmie.
Inną ciekawą analizą pozwalającą na diagnostykę stanu przekładni jest analiza EVAM (Evaluated Vibration Analysis Method). Polega ona na wybraniu zakresu widma pomiędzy głównymi GMF, a następnie obliczeniu średniej wartość amplitudy w tym zakresie. Wartość ta odpowiada stanowi przekładni (Rys. 7).

Rys. 7 Przykład zastosowania metody EVAM
Dla potrzeb analizy przedstawionej przekładni zębatej, metodę tą zastosowano dla przedziałów pomiędzy 1xGMF – 2xGMF (1050-1650 Hz) oraz 2xGMF – 3xGMF (1950-2550 Hz) (Rys. 8).
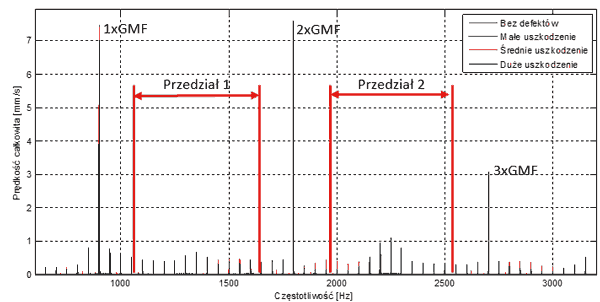
Rys. 8 Analizowane przedziały dla metody EVAM
Prążki znajdujące się w pobliżu częstotliwości GMF zostały pominięte, ponieważ mogą one wynikać z prawidłowej pracy układu, co mogłyby negatywnie wpływać na poprawność przeprowadzonej analizy. Na rysunku 9 przedstawiono wyniki analizy EVAM.
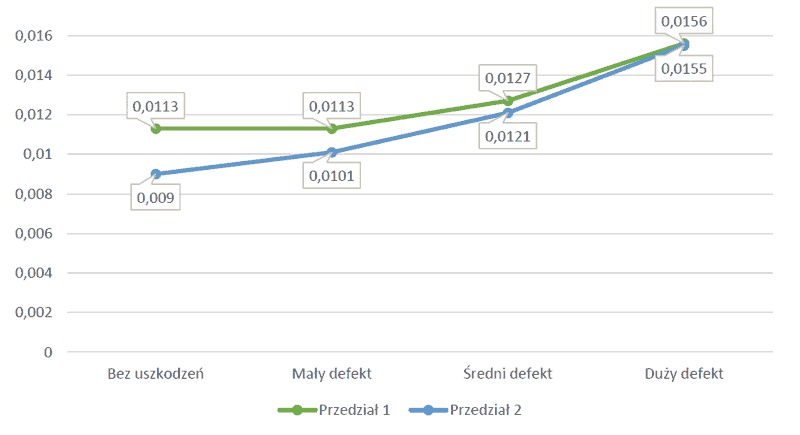
Rys. 9 Wykres wyliczonych parametrów dla metody EVAM
Metoda ta również okazała się skuteczna, gdyż można zauważyć, że wraz ze wzrostem uszkodzeń rośnie średnia wartość amplitudy sygnału znajdującego się pomiędzy głównymi GMF. Oczywiście aby metoda była możliwa do zastosowania, należałoby przeprowadzić dokładniejsze badania, w celu określenia poziomów, przy których występuje niebezpieczeństwo awarii. Zaletą tej metody jest jej stosunkowa prostota i szybkość zastosowania, natomiast główną wadą jest bardzo ogólne podejście do problemu. Podwyższone prążki pomiędzy głównymi harmonicznymi mogą oznaczać uszkodzenia kół zębatych, ale mogą to być również symptomy na przykład zużytych łożysk.
Obydwie wcześniejsze metody bazowały na analizie sygnałów w dziedzinie częstotliwości, jednak do wykrywania pęknięć u podstawy zęba można również posłużyć się analizą przebiegu czasowego. Na rysunku 10 przedstawiono wykresy przebiegów całkowitego przyśpieszenia oraz prędkości rejestrowanych na wale koła z wprowadzonym uszkodzeniem. Analizując sygnały, można zauważyć powtarzający się cyklicznie wzór, przedstawiony kolorem czerwonym.
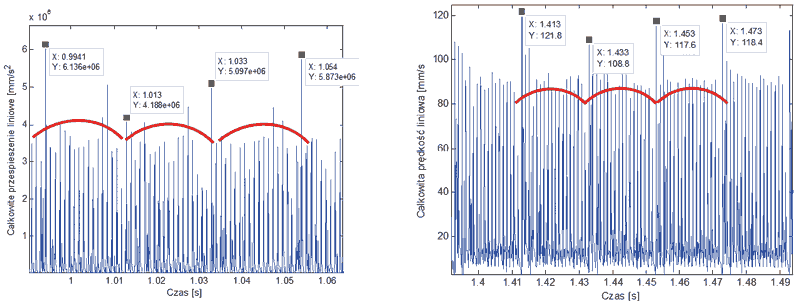
Rys. 10 Przebieg czasowy sygnału drganiowego z powtarzającym się wzorem
Odczytując z wykresów czas cyklu, otrzymujemy wartość około 0,02 sekundy. Wartość ta pochodzi od prędkości obrotowej uszkodzonego koła zębatego (50 Hz), którego jeden pełny obrót trwa 0,02s. Do modelu wprowadzono jedno uszkodzenie, dlatego cyklicznie powtarzająca się zależność może pochodzić od momentu zazębiania się uszkodzonego zęba. Powyższa analiza została przeprowadzona jedynie dla wycinka przebiegu przyśpieszenia. Aby przeanalizować cały dostępny sygnał, zdecydowano się na zastosowanie analizy cepstralnej.
Jest to jedna z metod analizy w dziedzinie częstotliwości. Cepstrum – to odwrotna transformata Fouriera widma sygnału wyrażonego w skali logarytmicznej. Zostaje uzyskana poprzez transformację (np. Fouriera) przeprowadzoną na widmie amplitudowym sygnału. Ponieważ widmo sygnału jest okresowe to maksimum cepstrum odpowiada częstotliwości podstawowej sygnału (Rys. 11).
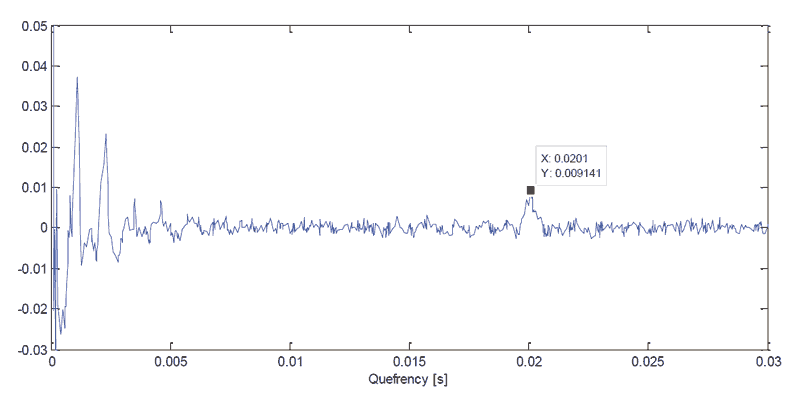
Rys. 11 Wynik analizy cepstralnej
Rozpatrując wynik analizy cepstralnej należy zwrócić szczególną uwagę na pierwsze występujące w sygnale maksimum. Określa ono częstotliwość podstawową sygnału. Maksima znajdujące się blisko zera zostają odrzucone z uwagi na niejednoznaczności występujące w początkowych fazach przebiegu sygnału. Poszukiwane przez nas ekstremum znajduje się w odległości 0,02s – czyli dokładnie takiej, jakiej spodziewaliśmy się po analizie teoretycznej (częstotliwość zazębiania się uszkodzonego zęba) oraz po okresowo powtarzających się wzorach na wykresach przyśpieszenia, jak również prędkości. Analiza cepstralna została przeprowadzona zarówno dla przebiegu prędkości, jak i przyspieszenia, dając takie same wyniki.
Podsumowanie
Uzyskane wyniki modelowania oraz symulacji komputerowych przekładni zębatych, przestawiają sposoby przeprowadzania analiz lokalnych uszkodzeń. Przedstawiony sposób podejścia do problemu jest złożony oraz czaso- i zasobochłonny, jednak po odpowiedniej optymalizacji metoda ta umożliwi generowanie wyników zbliżonych do pomiarów eksperymentalnych. Uzyskany w ten sposób sygnał może zostać wykorzystany w aplikacjach CBM (badanie bazujące na aktualnym stanie/zużyciu przekładni). Możliwość przeprowadzania badań na tego typu sygnale umożliwiłaby dokładniejszą oraz bardziej trafną diagnostykę przekładni. Sygnał drganiowy może być czasami bardzo trudny do uzyskania w tradycyjny sposób – podczas fizycznego pomiaru. Wykorzystując symulacje komputerowe, możliwe jest zamodelowanie i przeprowadzenie analizy przekładni zębatej przy pomocy metody elementów skończonych oraz dynamiki wielobryłowej. Ponadto, korzystając z podanych metod, możliwe jest wykrywanie symptomów uszkodzeń w postaci pęknięcia zęba u podstawy. Przedstawiony tok postępowania z sukcesem może również zostać wykorzystany do analiz bardziej skomplikowanych systemów.
Maciej Majerczak
Bibliografia
ADAMS 2015.1 Help
A. Jabłoński i T. Barszcz: Validation of vibration measurements for heavy duty machinery diagnostics, Mechanical Systems and Signal Processing, 38 (1) 2013
R. Randall: Vibration-based Condition Monitoring, John Wiley & Sons, 2011
C. Davidson: Flexible Body Integration using Adams and MSC. Nastran, online webinarium
J. Giesbers: Contact mechanics in MSC ADAMS, University of Twente, 2012
artykuł pochodzi z wydania 12 (135) grudzień 2018