Wyniki obliczeń
W wyniku przeprowadzenia analizy nieliniowej otrzymano obliczenie słabo skorelowane z eksperymentem. Model numeryczny próbki jest zbyt sztywny i osiąga mniejsze wartości naprężeń powyżej granicy plastyczności dla danych wartości odkształceń. Rozbieżność jest znaczna. Punkt przewężenia dla obu krzywych jest w podobnym zakresie.
HyperStudy do badania przestrzeni projektowej
Badanie przestrzeni projektowej (Design of Experiment) daje nam wskazówki na temat wpływu poszczególnych zmiennych na interesujące nas cechy. Pozwala uświadomić jakie są relacje między charakterystyką krzywej rozciągania, a zmiennymi projektowymi tj. moduł Younga, granica plastyczności, moduł umocnienia i wykładnik umocnienia. Dzięki temu można zweryfikować, w jakim stopniu parametry mają wpływ na zmienność charakterystyki naprężnie-odkształcenie.
W celu korelacji krzywej z symulacji i eksperymentu wybrano cztery punkty kontrolne, dla których narzędzie Hyperstudy i jego pełny algorytm czynnikowy (full factorial method) przyrównuje obie te krzywe. Algorytm ten szacuje wszelkie możliwe kombinacje wprowadzonych zmiennych. Wystarczy tylko podać pewien zakres szukanych wartości.
Zdefiniowanie punktów kontrolnych, które zaznaczono graficznie na rysunku 10, odbywa się za pomocą pewnych funkcji, które są wbudowane w panelu tworzenia wyrażeń (Expression Builder). Zawiera on listę matematycznych rozwiązań, które można wybrać, aby określić własności jakie chcemy osiągnąć.

Rys. 11 Metody badawcze przestrzeni projektowej
Na rysunku 12 przedstawiono wprowadzone interpolacje funkcji liniowej do obliczenia naprężeń dla 2- i 3-procentowego odkształcenia. W celu znalezienia maksymalnego naprężenia i odkształcenia, w punkcie przewężenia dla charakterystyki rozciągania, posłużono się maximum funkcji.

Rys. 12 Funkcje matematyczne Expression Builder
Wyniki obliczeń przestrzeni projektowej
Do oceny poszczególnych zmiennych najczęściej wykorzystywany jest diagram Pareto. Celem jest pokazanie najbardziej istotnych spośród dużej liczby czynników. Pojedyncze wartości parametrów reprezentowane są przez słupki w porządku malejącym. Na jej podstawie jesteśmy w stanie wskazać, które wprowadzone zmienne są istotne dla optymalizacji krzywej Johnsona-Cooka, a które należy zaniedbać. Na rysunku 13 wykres wskazuje, że moduł Younga ma znaczący wpływ na wprowadzony punkt kontrolny.
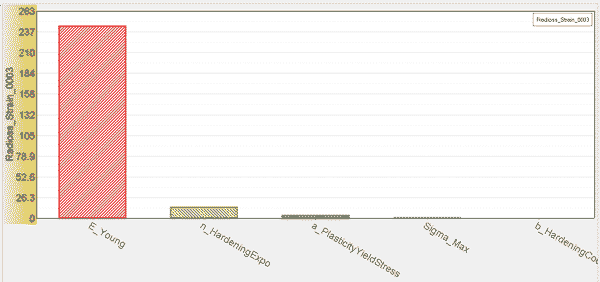
Rys. 13 Wykres Pareto dla sprężystej charakterystyki krzywej
To ma sens, z racji tego, że ten parametr wpływa na cześć sprężystą krzywej, gdzie zaistniały największe różnice. Influencja maksymalnego naprężenia jest nieistotna, ponieważ odnosi się do punktu kontrolnego powyżej puntu przewężenia, którego wybrane prawo materiałowe nie bierze pod uwagę. Rozważając te badania można dojść do wniosku, że bezpiecznie będzie pominąć ten parametr w przypadku optymalizacji.
Kalibracja materiału
Kolejny etapem będzie dopasowanie parametrów modelu materiałowego Johnsona-Cooka przy wykorzystaniu specjalnego narzędzia System Identification. Ten typ rozwiązania dąży do zmniejszenia sumy kwadratu błędu tj. różnicy między obliczeniem numerycznym a zadaną wartością docelową. Warto zauważyć, że przy tym rodzaju optymalizacji nie wprowadzamy żadnych równań czy funkcji ręcznie, lecz jednoznacznie wstawiamy pożądane wartości dla każdej odpowiedzi [6].
Ważnym aspektem jest także dobór metody optymalizacji opartej na aproksymacji. W zagadnieniu tym zbieżność rozwiązania można uzyskać dzięki zastosowaniu podejścia Global Response Surface Method, którą przedstawiono na rysunku 14.

Rys. 14 Zestawienie metod aproksymacji optymalizacji
Powierzchnia odpowiedzi jest adaptacyjnie aktualizowana poprzez nowe rozwiązania, by znaleźć lepsze dopasowanie modelu. Świetnie się nadaje do zagadnień związanych z kilkoma celami lub gdy zdefiniowanych jest wiele zmiennych projektowych. Jeśli analiza modelu jest czasochłonna, wtedy ta metoda jest dobrym rozwiązaniem. Dla krótkich analiz i dokładnych poszukiwań przestrzeni projektowej zaleca się podejście Genetic Algorithm lub Multi-Objective Genetic Algorithm [4, 5].
Wyniki i wnioski obliczeń optymalizacji
W wyniku optymalizacji uzyskano zadowalającą zbieżność w zakresie 1%. Na rysunku 15 łatwo zauważyć znaczącą różnicę przed i po optymalizacji. Charakterystyka modelu materiału dla próbki tytanu bardzo dobrze się koreluje z krzywą eksperymentalną.
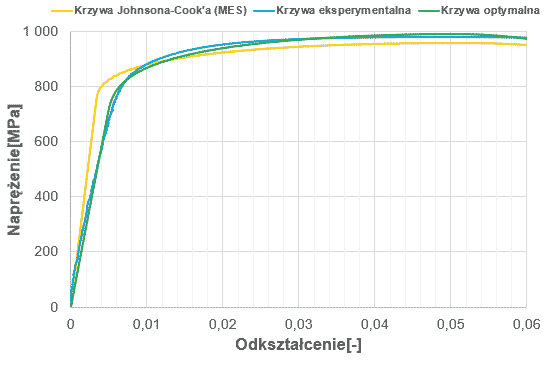
Rys. 15 Porównanie eksperymentu, krzywej Johnsona-Cooka przed i po optymalizacji
Wykorzystując badanie przestrzeni projektowej oraz optymalizację zamiast podejścia metodą prób i błędów, która jest tradycyjnym sposobem wykonywania kalibracji modelu, można zmniejszyć czas na kalibrację i zwiększyć jej jakość. Program HyperStudy ma specjalne metody optymalizacyjne, takie jak System Identification, w celu przyspieszenia procesu przygotowania symulacji.
Mateusz Oliwa
Ten adres pocztowy jest chroniony przed spamowaniem. Aby go zobaczyć, konieczne jest włączenie w przeglądarce obsługi JavaScript.
Aleksander Banaś
Ten adres pocztowy jest chroniony przed spamowaniem. Aby go zobaczyć, konieczne jest włączenie w przeglądarce obsługi JavaScript.
Radosław Wojtuszewski
Ten adres pocztowy jest chroniony przed spamowaniem. Aby go zobaczyć, konieczne jest włączenie w przeglądarce obsługi JavaScript.
Sekcja Techniczna Projektu Technologii Przyrostowych
PZL Mielec A Sikorsky Company
Literatura:
Beluch W., Burczyński T., Fedeliński P., John A., Kokot G., Kuś W. „Laboratorium z wytrzymałości materiałów”. Gliwice: Wydawnictwo Politechniki Śląskiej, 2002
Konowalski K. Statyczna próba rozciągania metali. Szczecin: Wydział Inżynierii Mechanicznej i Mechatroniki, Szczecin, 2015
Altair HyperWorks, Introduction to RADIOSS for Impact, Chapter 5: Material Laws and Characterization, 2016
https://altairhyperworks.com/hwhelp/Altair/2017/help/hst/hst.htm?hs_4200.htm
Altair HyperWorks, „HyperStudy” Altair Engineering, 2009
Kocer-Poyraz F. „Model Calibration Using Optimization Techniques”. Altair HyperWorks, 2012
artykuł pochodzi z wydania 9 (132) wrzesień 2018
Czytaj także:
- start
- Poprzedni artykuł
- 1
- 2
- Następny artykuł
- koniec









