Opublikowano: 26 lutego 2018

Coraz bardziej rozwijającym się segmentem rynku lotniczego stają się maszyny zwane High Performance Light Aircraft, a szczególnie High Speed Personal Jet. Dla dużej grupy klientów lekkie samoloty tłokowe są zbyt wolne, a tzw. odrzutowce funkcyjne – zbyt drogie. Ideałem jest maszyna łącząca zalety tych samolotów: łatwa w pilotażu, niezbyt droga w zakupie i utrzymaniu, a ponadto zapewniająca komfort kilku pasażerom.

Ryszard Romanowski

Powinien to być lekki samolot odrzutowy spełniający wymogi General Aviation. Niestety, oferta jest niewielka. Do niedawna prezentowano prototypy zaledwie trzech maszyn budzących duże zainteresowanie potencjalnych klientów. Jedną z nich jest austriacki Diamond D-Jet, który na razie nie doczekał się produkcji seryjnej, z powodów finansowych. Firma Diamond obiecuje, że niebawem kontynuować będzie dalsze prace zmierzające do uzyskania certyfikatów i rozpoczęcia produkcji seryjnej. Kolejnym jest polski Flaris, opisywany przed rokiem w naszym magazynie. Maszyna firmy Metal Master jest w fazie testowej.

Pozostał Cirrus Vision SF50, który po licznych finansowych i własnościowych zawirowaniach przeszedł procesy certyfikacji, zarówno w amerykańskiej FAA, jak i europejskiej EASA, i trafił do produkcji seryjnej. Maszyna nazywana potocznie Vision Jet jest pierwszym najmniejszym certyfikowanym cywilnym odrzutowcem. Jedna z dwóch europejskich premier tego samolotu odbyła się 23 września ubiegłego roku na poznańskim lotnisku Ławica. Organizatorem wydarzenia było centrum treningowe Cirrusa – Aero Poznań. W stolicy Wielkopolski mieści się przedstawicielstwo Cirrusa pod nazwą Cirrus Poland & Baltic oraz ośrodek szkoleniowy dla pilotów, dysponujący jednym z czterech na świecie symulatorów. Pozostałe trzy znajdują się w USA. Symulatory te nie odbiegają technicznie od najnowocześniejszych urządzeń przeznaczonych do szkoleń pilotów samolotów pasażerskich.
Znana z produkcji doskonałych lekkich samolotów tłokowych firma Cirrus rozpoczęła projekt nazwany The Jet, w celu zapełnienia rynkowej luki i zaoferowania pilotom bardzo cenionych modeli SR20 i SR22, szybkiej odrzutowej maszyny, podobnie jak tamte – mało kłopotliwej i łatwej w pilotażu. Przedstawiono samolot wykonany w całości z kompozytu, z kabiną mieszczącą siedem osób. Pierwotną nazwę projektu szybko zastąpioną nową: Vision SF50.

cały artykuł dostępny jest w wydaniu 1/2 (124/125) styczeń-luty 2018

Opublikowano: 26 lutego 2018

Pod względem innowacji w produkcji i gospodarce polskie przedsiębiorstwa należą do najmniej aktywnych w Unii Europejskiej. Według instytucji PRO INNO Europe, założonej przez Komisję Europejską do badania rozwoju innowacyjności, polskie przedsiębiorstwa zajmują miejsca w trzeciej dziesiątce państw unijnych.

Aleksander Łukomski

Według Ministerstwa Gospodarki największą barierą dla rozwoju innowacyjności polskich przedsiębiorstw są wysokie koszty prowadzenia badań naukowych oraz niechęć przedsiębiorców do podejmowania ryzyka związanego z wprowadzaniem nowych rozwiązań i produktów. Dochodzi do tego brak koordynacji pomiędzy badaniami naukowymi, a potrzebami przedsiębiorstw.
Innowacyjność związana jest z postępem technicznym, który oznacza zmianę danego poziomu techniki na wyższy, przy jednoczesnym spełnieniu czterech kryteriów:

• Techniczny. Lepsze właściwości techniczno-eksploatacyjne musi charakteryzować nowy poziom techniki;
• Ekonomiczny. Wyższy poziom techniki jest wtedy, gdy łączne nakłady na jednostkę produktu są mniejsze;
• Społeczny. Stosowana technika powinna być bardziej „przyjazna” dla użytkownika;
• Ekologiczny. Podejmowane działania inżynierskie nie mogą szkodzić ekosferze: wodzie, powietrzu, glebie; urządzenia powinny być cichsze.

Podstawą postępu technicznego jest inwencja, a wykorzystanie tej inwencji to innowacja w postaci opracowania, wdrożenia, upowszechnienia prototypu lub nowego rozwiązania. Nowe rozwiązanie nie jest jednak jeszcze innowacją, dopóki nie ma ono praktycznego zastosowania. Rozróżnia się kilka rodzajów innowacji w zależności od kryterium:

• kryterium oryginalności:
  -kreatywna, czyli twórcza, odkrywcza;
  -imitująca – odtwórcza, naśladowcza;
• kryterium systemu pobudzania innowacji:
  -podażowa, jako wynik odkryć, wynalazków stymulowanych przez rozwój nauki i techniki,
  -popytowa, stymulowana przez samo przedsiębiorstwo i rynek;
• kryterium efektów:
  -produktowa, która związana jest z rentownością;
  -procesowa, nie jest tożsama z technologią; zmiana technologii może być jednym z elementów innowacji procesowej;
  -czynnikowa, odnosząca się do nowych czynników potrzebnych do wytwarzania towarów np. nowe elementy infrastruktury społecznej.

Bardzo często w ramach funduszy europejskich przeznaczonych na innowacje przedsiębiorstwa kupują nowe maszyny np. frezarki, koparki itp.

Fot. 1    Produkcja małych skrzynek metalowych w sposób tradycyjny

Może w niektórych takich przypadkach występuje nawet coś zbliżonego do innowacji, jakaś zmiana w przedsiębiorstwie w tym kierunku, ale bardzo często nie są to w rzeczywistości żadne innowacje.

cały artykuł dostępny jest w wydaniu 1/2 (124/125) styczeń-luty 2018

Opublikowano: 26 lutego 2018

Podstawą definicji każdego mechanizmu jest określenie par kinematycznych. Są jednak takie mechanizmy, w których kontakt pomiędzy jego częściami nie jest ciągły i dlatego definicja pary kinematycznej nie jest oczywista. Na przykład mechanizm maltański (znany także jako mechanizm genewski – zwłaszcza w literaturze anglojęzycznej) przekształca ciągły ruch obrotowy członu napędowego na okresowo przerywany ruch obrotowy członu napędzanego – trzpień koła napędowego wchodzi kolejno w kanałki koła napędzanego powodując jego okresowy obrót o kąt zależny od liczby kanałków.

Andrzej Wełyczko

Rozważmy definicję takiego mechanizmu i symulację jego ruchu w systemie CATIA V5 dla koła napędzanego z sześcioma kanałkami (Rys. 1).

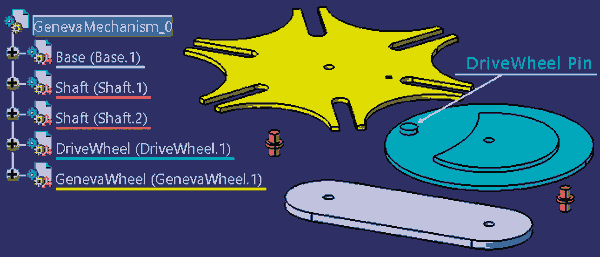
Rys. 1

Definiowanie geometrii poszczególnych części tego zespołu pominę, aby skupić się na temacie głównym. Jeśli części zespołu mamy zdefiniowane, to podstawowym zadaniem jest ustalenie ich wzajemnego położenia w przestrzeni roboczej. Precyzyjną definicję wzajemnego położenia części wykonujemy w środowisku Assembly Design (Rys. 2), aplikując wymagane więzy (Constraints): Fix, Coincidence, Contact, itd. Dla uproszczenia zastosowałem sztywne połączenie (FixTogether) wałków (Shaft.1 i Shaft.2) odpowiednio z kołem napędowym (DriveWheel.1) i napędzanym (GenevaWheel.1).

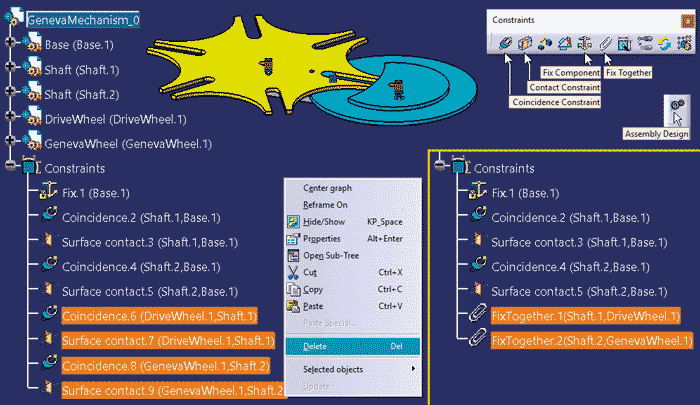
Rys. 2

Relacje typu Constraints zdefiniowane w środowisku Assembly Design nie są równoważne z definicją par kinematycznych, bo te są definiowane w środowisku Digital Mock-Up Kinematics. Jeśli w środowisku Assembly Design zdefiniowano relacje typu Constraints, to definicje par kinematycznych można uzyskać automatycznie za pomocą polecenia Assembly Constraints Conversion (Rys. 3).

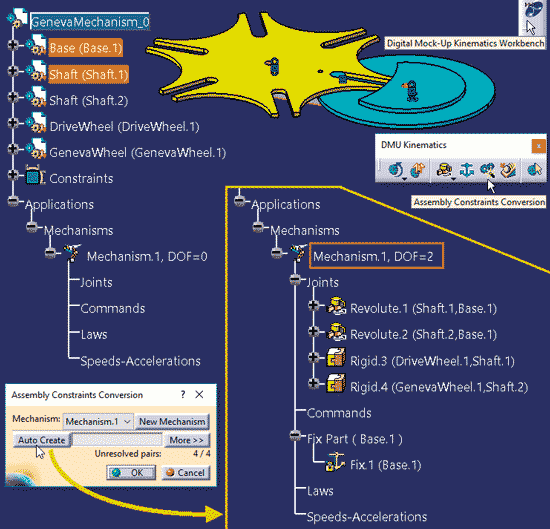
Rys. 3

W rezultacie takiej konwersji otrzymujemy cztery pary kinematyczne (Revolute.1, Revolute.2, Rigid.3 i Rigid.4) oraz element nieruchomy (Fix Part). Mechanizm ma dwa stopnie swobody (DOF = 2) i dlatego nie można jeszcze wykonać symulacji jego ruchu. Trzeba przecież określić jak ruch jest przenoszony z koła DriveWheel.1 na koło GenevaWheel.1 oraz zdefiniować element napędowy (tu oczywiście DriveWheel.1).
Naturalną (choć nie najprostszą) metodą powiązania ruchu kół DriveWheel.1 i GenevaWheel.1 jest wyznaczenie trajektorii ruchu osi trzpienia napędowego (DrivePinCenterPoint na rysunku 4) względem koła napędzanego.

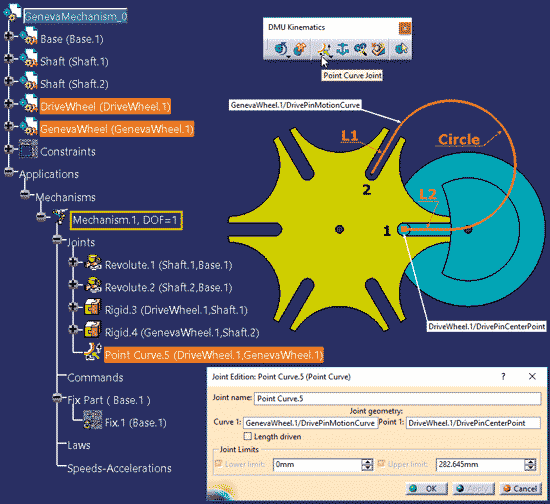
Rys.4

Zadanie to tylko z pozoru jest trudne, ponieważ:

• w początkowej fazie ruchu trzpień napędowy porusza się w osi kanałka 1 – odcinek liniowy L1;
• w końcowej fazie ruchu trzpień napędowy porusza się w osi kanałka 2 – odcinek liniowy L2;
• pomiędzy tymi fazami trzpień porusza się po łuku okręgu (tu Circle), który jest styczny do odcinków L1 i L2.

Wniosek: punkt DrivePinCenterPoint porusza się po krzywej DrivePinMotionCurve, którą tworzą trzy segmenty: L1, Circle i L2. Punkt DrivePinCenterPoint musi być zdefiniowany w modelu DriveWheel, a krzywa DrivePinMotionCurve w modelu GenevaWheel.
Wałek Shaft.1 ma możliwość obrotu względem podstawy (tu: Base.1) i jest jednocześnie sztywno połączony z kołem DriveWheel.1. Z tego powodu parametr napędowy Command.1 musi być częścią definicji pary kinematycznej Revolute.1(Shaft.1, Base.1), bo ta ustala położenie wałka Shaft.1 względem podstawy Base.1 (Rys. 5).

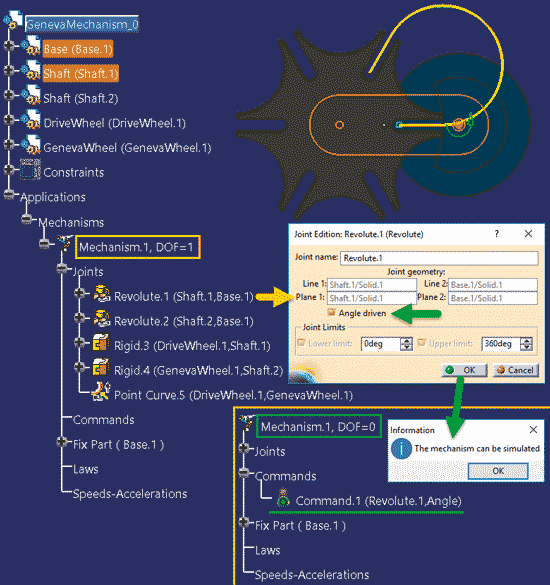
Rys. 5

Symulacja ruchu mechanizmu może być wykonana za pomocą polecenia Simulation with Commands (Rys. 6):

• dla 0° ≤ Command.1 ≤ 60° kąt obrotu koła napędzanego zmienia się od 0° do 30°,
• dla 60° < Command.1 < 300° kąt obrotu koła napędzanego jest stały i wynosi 30°,
• dla 300° ≤ Command.1 ≤ 360° kąt obrotu koła napędzanego zmienia się od 30° do 60°.

Rys. 6

Taka definicja mechanizmu ma jednak istotną wadę – nie jest możliwa symulacja ruchu dla więcej niż jednego obrotu koła napędowego. Dlaczego? Jeśli, na przykład, zdefiniujemy trajektorię ruchu trzpienia koła napędowego dla dwóch pełnych obrotów tego koła (Rys. 7A), to taka krzywa jest kompletnie nieużyteczna. I nawet jeśli algorytm definiowania pary kinematycznej typu Point Curve nie generuje błędu i pozwala na symulację ruchu mechanizmu, to ta zatrzymuje się dla Command.1 = 300°, czyli w punkcie, w którym łączą się trzy segmenty zadanej trajektorii ruchu trzpienia (odcinek liniowy i dwa łuki). Analiza krzywej wskazuje na błąd typu Manifold (Rys. 7B) w tym właśnie punkcie i dlatego symulacja ruchu mechanizmu dla Command.1 > 300° nie jest możliwa.

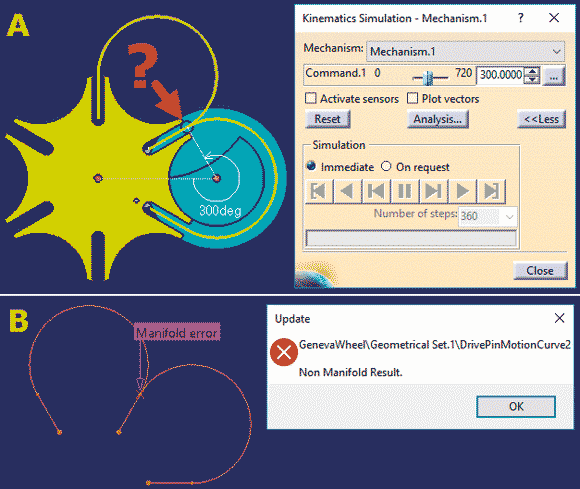
Rys. 7

Sytuacja nie jest jednak beznadziejna, bo wiemy (Rys. 8) jak zmienia się kąt obrotu koła napędzanego (Revolute.2\Angle) w funkcji zmian kąta obrotu koła napędowego (Revolute.1\Angle). Na podstawie takich danych można zdefiniować geometryczne prawa zmienności tych kątów: ręcznie (na przykład w środowisku Sketcher) lub półautomatycznie (eksport wartości tych kątów do pliku dyskowego i rekonstrukcja funkcji Revolute.2\Angle = f(Revolute.1\Angle) – na przykład za pomocą dedykowanego makra).

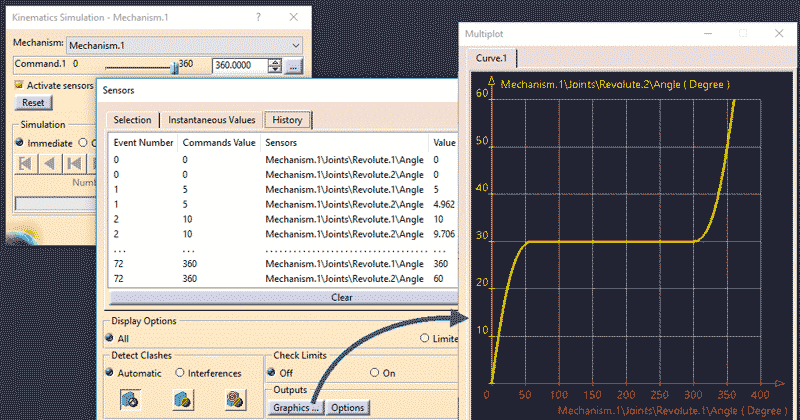
Rys. 8

Rozważmy kolejną wersję mechanizmu maltańskiego (Rys. 9), w którym usunięto parę kinematyczną Point Curve.5 oraz dodano kolejny parametr napędowy (tu: Command.2), odpowiedzialny za obrót koła GenevaWheel. Teoretycznie można wykonać symulację ruchu takiego mechanizmu bez praw zmienności i powiązania parametrów napędowych, ale w takim przypadku obrót koła napędzanego jest niezależny od obrotu koła napędowego. Jeśli zdefiniujemy wykresy (prawa) zmienności parametrów Command.1 oraz Command.2, to możliwa będzie symulacja ruchu mechanizmu dla dowolnej liczby obrotów koła napędowego.

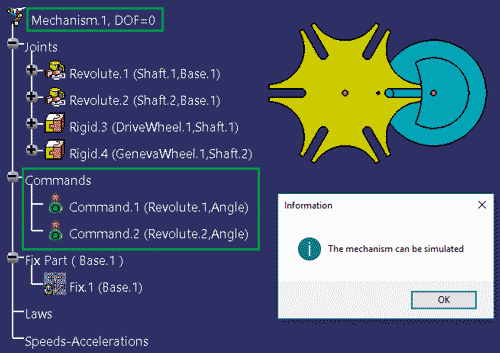
Rys. 9

Jak skonstruować wykresy zmian parametrów Command.1 i Command.2 w czasie? Odpowiedź jest raczej oczywista (Rys. 10):

• Koło napędowe obraca się ze stałą prędkością kątową (załóżmy ω = 1°/s = 1/6 obr/min). Wartość kąta Revolute.1\Angle (czyli Command.1) zmienia się liniowo – wykres zmian tego parametru zdefiniowano jako szkic DriveWheel.
• Koło napędzane obraca się ze zmienną prędkością – wykres zmian kąta Revolute.2\Angle (czyli Command.2) zdefiniowano jako szkic GenevaWheel.

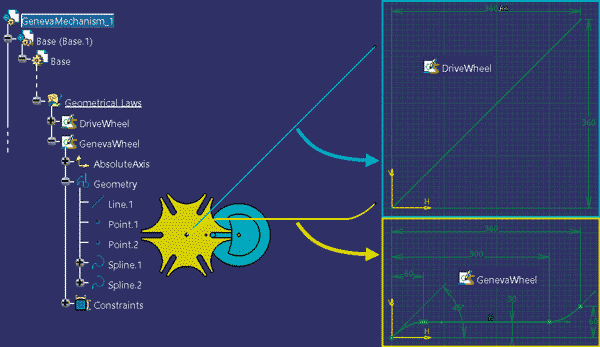
Rys. 10

Oba wykresy zostały zdefiniowane w nieruchomej części mechanizmu – tu: komponent Base.1. Struktura szkicu GenevaWheel nie jest skomplikowana: odcinek liniowy (Line.1) oraz dwie krzywe typu spline (Spline.1 i Spline.2). Zmiana wartości Revolute.2\Angle w zakresach 0°÷30° oraz 30°÷60° (reprezentowana przez krzywe Spline.1 i Spline.2) nie jest liniowa i dlatego trzeba zastanowić się ile punktów zastosować w definicji tych krzywych oraz jakie są współrzędne tych punktów. Najprostsze ale równocześnie najmniej dokładne rozwiązanie to dwa punkty skrajne z zadanymi warunkami styczności dla każdej krzywej spline.
Współrzędne punktów wewnętrznych krzywych Spline.1 i Spline.2 można wyznaczyć na podstawie konstrukcji geometrycznej (Rys. 11).

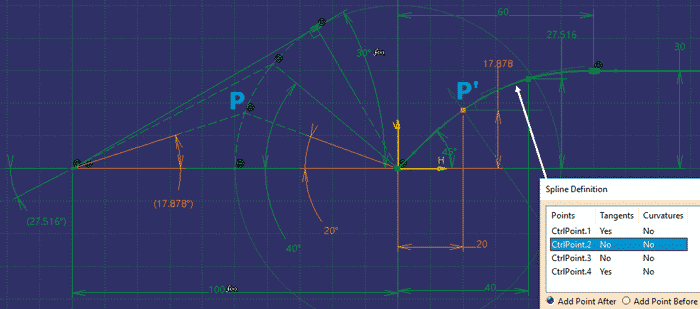
Rys. 11

Zainteresowanych analizą geometryczną mechanizmu maltańskiego odsyłam do literatury fachowej. Tu ograniczę się tylko do krótkiego opisu:

• Dla kąta Command.1 = 20° punkt P (oś trzpienia napędowego) określa wartość kąta Command.2 = 17,878°.
• Punkt P’ (odpowiednik punktu P) na krzywej Spline.1 (czyli punkt CtrlPoint.2) ma współrzędne: H = 20mm, V = 17,878mm.

Oczywiście im większa będzie liczba punktów wewnętrznych krzywych Spline.1 i Spline.2, tym bardziej szkic GenevaWheel będzie zbliżony do rzeczywistego wykresu zmian kąta Revolute.2\Angle.
Jeśli geometryczna definicja zmienności parametrów napędowych mechanizmu jest gotowa, to za pomocą polecenia Link (okno Command Edition na rysunku 12) można powiązać parametr napędowy z odpowiednim szkicem – tu: Command.1 ze szkicem DriveWheel. Podobna operacja musi być powtórzona, aby powiązać Command.2 ze szkicem GenevaWheel.

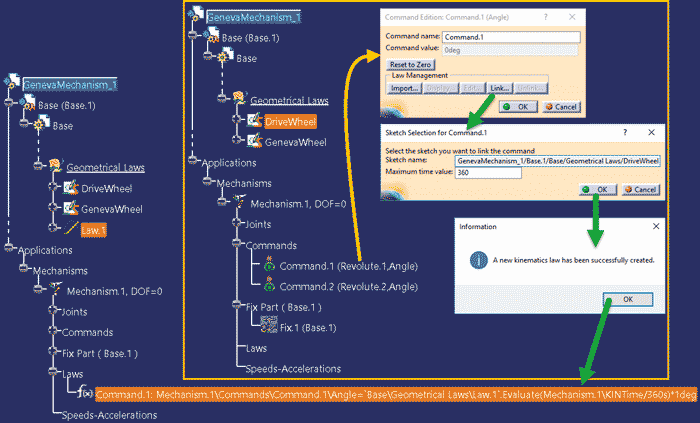
Rys. 12

W rezultacie wykonania tych poleceń (Rys. 13) w strukturze zespołu zostały utworzone dwa prawa zmienności (Law.1 i Law.2) oraz dwie formuły obliczeniowe do wyznaczenia wartości parametrów napędowych Command.1 i Command.2.

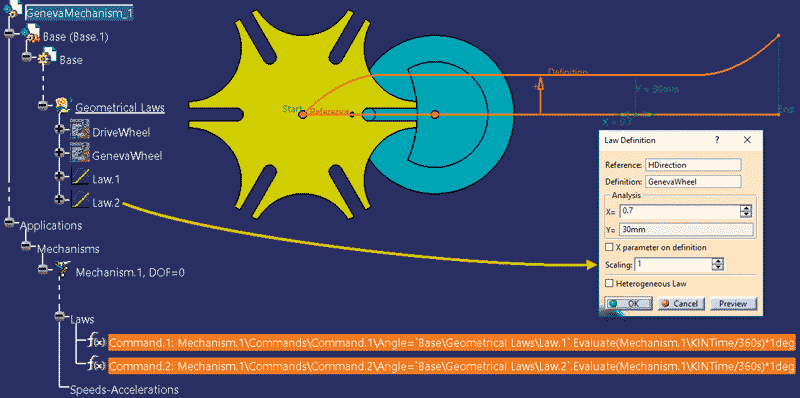
Rys. 13

Mechanizm jest gotowy do symulacji ruchu – w tym przypadku zastosujemy polecenie Simulations with Laws (Rys. 14). Poza samą symulacją warto czasami analizować zmiany wartości wybranych parametrów (okno Sensors zakładka History) lub wykres ich zmian (okno Multiplot) – choćby po to, by potwierdzić poprawność definicji mechanizmu.

Rys. 14

Jeśli trzeba wykonać symulację ruchu dla kilku obrotów koła napędowego (na przykład dla sześciu obrotów koła DriveWheel.1 uzyskamy jeden pełny obrót koła GenevaWheel.1), to trzeba odpowiednio zmodyfikować prawa zmienności, czyli (Rys. 15):

• szkic DriveWheel – wymiary 360 (patrz Rys.10) zmienić na 6*360=2160,
• szkic GenevaWheel – cały szkic skopiować pięć razy w taki sposób, aby zapewnić jego ciągłość (punkt początkowy kolejnej kopii jest zgodny z punktem końcowym poprzedniej).

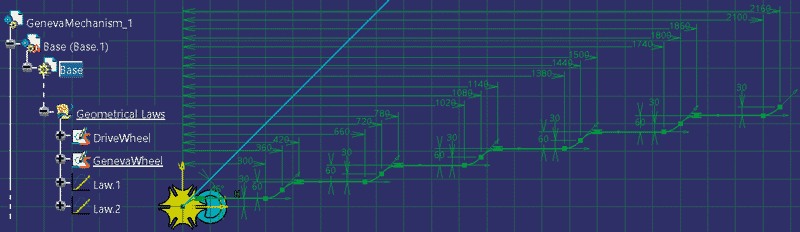
Rys. 15

Prawa zmienności mogą być także zdefiniowane analitycznie, za pomocą polecenia Rule w środowisku Knowledge Advisor. W takim przypadku należy zastosować równanie (Rys. 16) i w modelu pokazanym na rysunku 9 zdefiniować dwie zasady konstrukcyjne (DriveWheel oraz GenevaWheel na rysunku 17), w których Command.1\Angle jest odpowiednikiem kąta α, a Command.2\Angle jest odpowiednikiem kąta β.

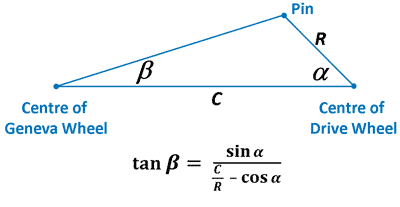
Rys. 16

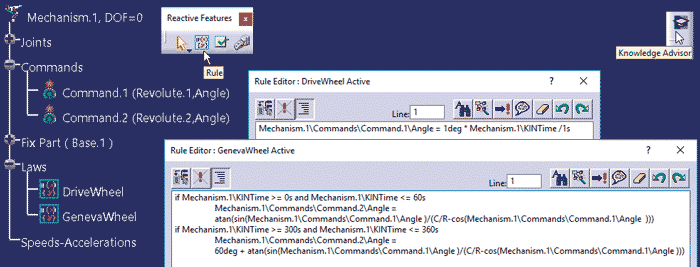
Rys. 17

Jeśli koło napędowe ma wykonać więcej niż jeden obrót (tu: sześć obrotów), to należy odpowiednio zmodyfikować zasadę GenevaWheel (Rys. 18).

Rys. 18

W rezultacie model mechanizmu maltańskiego jest gotowy do symulacji w zakresie zdefiniowanym przez GenevaWheel (Rys. 19). Jeśli w modelu zostanie zdefiniowana odpowiednia reakcja (obiekt Reaction) albo makro, to treść tej zasady konstrukcyjnej może być automatycznie generowana dla zadanych wartości parametrów (liczba kanałków koła napędzanego N i odległość osi kół C). Symulacja ruchu mechanizmu zdefiniowanego tą metodą jest precyzyjna, bo odwołuje się do teoretycznego modelu mechanizmu maltańskiego (patrz: równanie na rysunku 16).

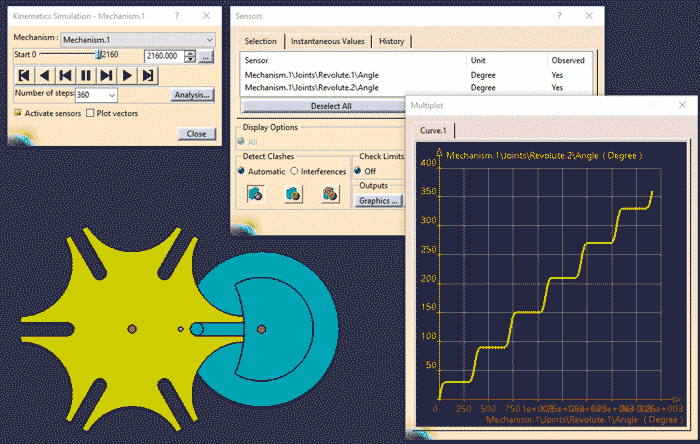
Rys. 19

Którą z opisanych wyżej metod zastosować? Wybór zależy od wymaganej dokładności i zakresu symulacji oraz... dostępnych licencji systemu CATIA V5.

Andrzej Wełyczko

artykuł pochodzi z wydania 1/2 (124/125) styczeń-luty 2018

Opublikowano: 26 lutego 2018

W układach smarowania przekładni i w przeprowadzonych dalej obliczeniach zakłada się, że mamy do czynienia z przepływami laminarnymi. Założenie to jest wynikiem stosowania niewielkich ciśnień, wynoszących od 0,1 - 0,7 MPa (1-7 bar) [1] i wynikających z nich niewielkich prędkości przepływu.

Jerzy Mydlarz

Dla wszystkich dalszych rozważań przyjęto założenie, że mamy do czynienia z laminarnym ruchem cieczy.
Przyjęta dalej metodyka postępowania została ujęta w punktach.

Opracowanie schematu obiegowego układu smarowania
Schemat kinematyczny przekładni pokazano na rysunku 1.

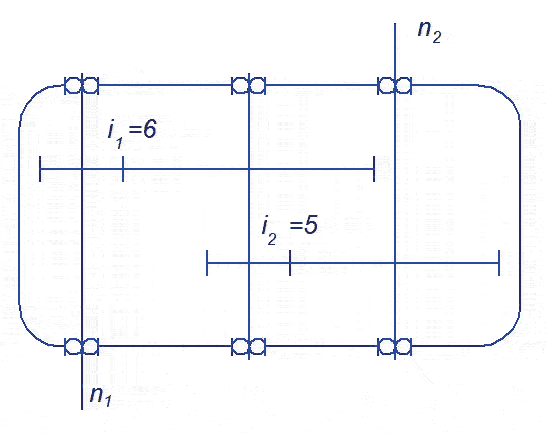
Rys. 1

Schemat ten ułatwi nam zidentyfikowanie wszystkich punktów, do których będzie doprowadzany olej. Przekładnia przedstawiona na schemacie, to przekładnia z poprzednich przykładów, o następujących parametrach:
Moc przenoszona     30 kW
Przełożenie całkowite     i_c = 30
Przełożenie pierwszego stopnia     i₁ = 6
Przełożenie drugiego stopnia     i₂ = 5
Koncepcję całego obiegowego układu smarowania dwustopniowej przekładni walcowej przedstawiono na rysunku 2.
Zbilansowanie zapotrzebowania na olej w przekładni
Wyznaczone w części 2 artykułu zapotrzebowanie oleju do chłodzenia i smarowania przekładni wynosi V_o’ = 4,7 l/min. Wyznaczone w części 3 zapotrzebowanie oleju do smarowania i chłodzenia jednego łożyska 6309 wynosi Q_oł = 0,1 l/min. Zatem całkowite zapotrzebowanie przekładni na olej wynosi:
Q_c = V_o’ + 6·Q_oł = 4,7 + 0,6 = 5,3 l/min = 88,3 cm³/s
Q_c = 88,3 cm³/s

cały artykuł dostępny jest w wydaniu 1/2 (124/125) styczeń-luty 2018